
已知函数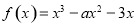
(1)若 在区间[1,+∞)上是增函数,求实数a的取值范围;
在区间[1,+∞)上是增函数,求实数a的取值范围;
(2)若x=-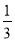 是
是 的极值点,求
的极值点,求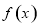 在[1,a]上的最大值;
在[1,a]上的最大值;
(3)在(2)的条件下,是否存在实数b,使得函数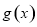 =bx的图象与函数
=bx的图象与函数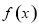 的图象恰有3个交点,若存在,请求出实数b的取值范围;若不存在,试说明理由.
的图象恰有3个交点,若存在,请求出实数b的取值范围;若不存在,试说明理由.
(1)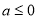 ;(2)
;(2)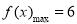 ;(3)
;(3)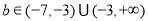
【解析】
试题分析:(1) 在区间[1,+∞)上是增函数
在区间[1,+∞)上是增函数 在区间[1,+∞)上恒成立
在区间[1,+∞)上恒成立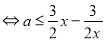
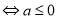 ;
;
(2)由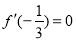 得
得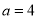 ,判定函数的单调性,可知函数的最大值为
,判定函数的单调性,可知函数的最大值为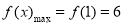 ;
;
(3)两个函数有三个不同的公共点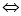 方程
方程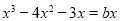 恰有三个不同的实根
恰有三个不同的实根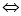
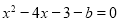 有两个不同非零实根
有两个不同非零实根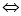
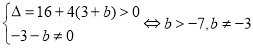 。
。
试题解析:(1) ,∵f(x)在[1,+∞)上是增函数,
,∵f(x)在[1,+∞)上是增函数,
∴在[1,+∞)上恒有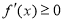 ,即3x
,即3x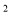 -2ax-3≥0在[1,+∞)上恒成立.则必有
-2ax-3≥0在[1,+∞)上恒成立.则必有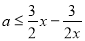 且
且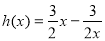 在区间[1,+∞)上是增函数,又
在区间[1,+∞)上是增函数,又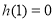 ,∴
,∴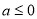 .
.
(2)依题意,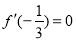 ,即
,即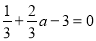 ,∴
,∴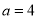 ,
,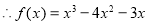 .
.
令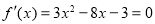 ,得
,得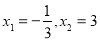 .
.
则当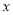 变化时,
变化时, 的变化情况如下表:
的变化情况如下表:
| 1 | (1,3) | 3 | (3,4) | 4 |
| - | 0 | + | ||
| -6 | ↘ | -18 | ↗ | -12 |
∴f(x)在[1,4]上的最大值是f(1)=-6.
(3)函数g(x)=bx的图象与函数f(x)的图象恰有3个交点,即方程x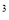 -4x
-4x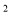 -3x=bx恰有3个不等实根
-3x=bx恰有3个不等实根
∴x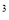 -4x
-4x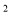 -3x-bx=0,∴x=0是其中一个根,∴方程x
-3x-bx=0,∴x=0是其中一个根,∴方程x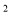 -4x-3-b=0有两个非零不等实根,
-4x-3-b=0有两个非零不等实根,
∴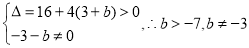
∴存在符合条件的实数b,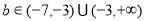
考点:函数与导数,函数单调生、最值、函数与方程。


 科学实验活动册系列答案
科学实验活动册系列答案科目:高中数学 来源:2014-2015学年上海市长宁区高三上学期教学质量检测文科数学试卷(解析版) 题型:填空题
已知 的展开式中的常数项为
的展开式中的常数项为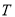 ,
,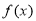 是以
是以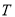 为周期的偶函数,且当
为周期的偶函数,且当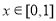 时,
时, ,若在区间
,若在区间 内,函数
内,函数 有4个零点,则实数
有4个零点,则实数 的取值范围是 .
的取值范围是 .
查看答案和解析>>
科目:高中数学 来源:2014-2015学年陕西省高三教学质量检测一理科数学试卷(解析版) 题型:选择题
若过点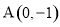 的直线
的直线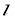 与圆
与圆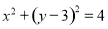 的圆心的距离记为
的圆心的距离记为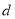 ,则
,则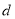 的取值范围为( )
的取值范围为( )
A.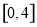 B.
B.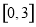 C.
C. D.
D.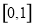
查看答案和解析>>
科目:高中数学 来源:2014-2015学年内蒙古巴彦淖尔市高三上学期期中考试文科数学试卷(解析版) 题型:填空题
在等比数列{ }中,各项都是正数,且3
}中,各项都是正数,且3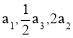 成等差数列,则
成等差数列,则 =______.
=______.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年内蒙古巴彦淖尔市高三上学期期中考试文科数学试卷(解析版) 题型:选择题
在等差数列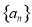 中,若
中,若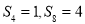 ,则
,则 的值为( )
的值为( )
A.9 B.12 C.16 D.17
查看答案和解析>>
科目:高中数学 来源:2014-2015学年广西梧州、崇左两市联考高三上学期摸底文科数学试卷(解析版) 题型:解答题
在直角坐标系xOy中,以原点O为极点,x轴的非负半轴为极轴建立极坐标系,已知圆C的圆心的极坐标为( ,
, ),半径r=
),半径r= ,点P的极坐标为(2,π),过P作直线l交圆C于A,B两点.
,点P的极坐标为(2,π),过P作直线l交圆C于A,B两点.
(1)求圆C的直角坐标方程;
(2)求|PA||PB|的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com