
| A. | 1.2 | B. | 1.3 | C. | 1.4 | D. | 1.5 |
分析 根据题意,所给的平均数为5,由平均数公式可得$\overline{x}$=$\frac{3+4+4+x+5+6+6+7}{8}$=5,解可得x=5,将x的值代入方差计算公式即可得答案.
解答 解:根据题意,数据3,4,4,x,5,6,6,7的平均数为5,
则有$\overline{x}$=$\frac{3+4+4+x+5+6+6+7}{8}$=5,解可得x=5,
则样本的方差S2=$\frac{1}{8}$[(3-5)2+(4-5)2+(4-5)2+(5-5)2+(5-5)2+(6-5)2+(6-5)2+(7-5)2]=$\frac{12}{8}$=1.5;
故选:D.
点评 本题考查方差的计算,关键是掌握方差的计算公式并准确计算.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
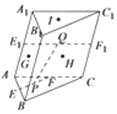 如图,在三棱柱ABC-A1B1C1中,E,F,E1,F1分别为棱AB,AC,AA1,CC1的中点,点G,H分别为四边形ABB1A1,BCC1B1对角线的交点,点I为△A1B1C1的外心,P,Q分别在直线EF,E1F1上运动,则在G,H,I,这三个点中,动直线PQ( )
如图,在三棱柱ABC-A1B1C1中,E,F,E1,F1分别为棱AB,AC,AA1,CC1的中点,点G,H分别为四边形ABB1A1,BCC1B1对角线的交点,点I为△A1B1C1的外心,P,Q分别在直线EF,E1F1上运动,则在G,H,I,这三个点中,动直线PQ( )| A. | 只可能经过点I | B. | 只可能经过点G,H | ||
| C. | 可能经过点G,H,I | D. | 不可能经过点G,H,I |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某公司2017年元旦晚会现场,为了活跃气氛,将在晚会节目表演过程中进行抽奖活动.
某公司2017年元旦晚会现场,为了活跃气氛,将在晚会节目表演过程中进行抽奖活动.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
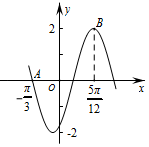 函数f(x)=Asin(ωx+ϕ),($A>0,ω>0,-\frac{π}{2}<ϕ<\frac{π}{2}$)的部分 图象如图所示,则函数f(x)的解析式为f(x)=2sin(2x$-\frac{π}{3}$).
函数f(x)=Asin(ωx+ϕ),($A>0,ω>0,-\frac{π}{2}<ϕ<\frac{π}{2}$)的部分 图象如图所示,则函数f(x)的解析式为f(x)=2sin(2x$-\frac{π}{3}$).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| t | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
| y | 5 | 7.5 | 5 | 2.5 | 5 | 7.5 | 5 | 2.5 | 5 |
| A. | $y=5+\frac{5}{2}sin\frac{π}{12}t,t∈[0,24]$ | B. | $y=5+\frac{5}{2}sin(\frac{π}{12}t+\frac{π}{2}),t∈[0,24]$ | ||
| C. | $y=5+\frac{5}{2}sin\frac{π}{6}t,t∈[0,24]$ | D. | $y=5+\frac{5}{2}sin(\frac{π}{6}t+π),t∈[0,24]$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com