
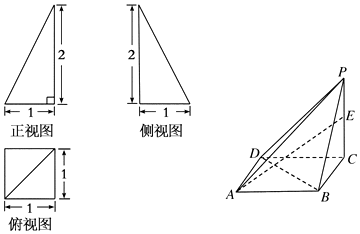
分析 (1)由三视图可知,四棱锥中,PC⊥底面ABCD底面ABCD是边长为1的正方形,PC=2,由此能求出四棱锥P-ABCD的体积.
(2)连接AC,推导出BD⊥平面PAC,由此能求出当E在PC上运动时,BD⊥AE恒成立.
解答 解:(1)由三视图可知,四棱锥中,PC⊥底面ABCD,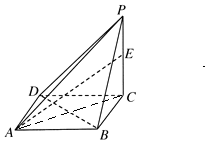
底面ABCD是边长为1的正方形,PC=2,
∴四棱锥P-ABCD的体积VP-ABCD=$\frac{1}{3}$•PC•S底=$\frac{1}{3}$×2×1=$\frac{2}{3}$.
(2)不论点E在何位置,都有BD⊥AE成立.
证明如下:连接AC,∵BD⊥AC,BD⊥PC,且AC∩PC=C,
∴BD⊥平面PAC,
当E在PC上运动时,AE?面PAC,
∴BD⊥AE恒成立.
点评 本题考查几何体的体积的求法,考查线线垂直的判断与证明,考查空间中线线、线面、面面间的位置关系等基础知识,考查推理论证能力、运算求解能力、空间想象能力,考查化归与转化思想、数形结合思想,是中档题.


 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:高中数学 来源: 题型:解答题
 电视传媒公司为了了解某地区电视观众对某类体育节目的收视情况,随机抽取了100名观众进行调查,其中女性有55名.下面是根据调查结果绘制的观众日均收看该体育节目时间的频率分布直方图,将日均收看该体育节目时间不低于40分钟的观众称为“体育迷”,已知“体育迷”中有10名女性.
电视传媒公司为了了解某地区电视观众对某类体育节目的收视情况,随机抽取了100名观众进行调查,其中女性有55名.下面是根据调查结果绘制的观众日均收看该体育节目时间的频率分布直方图,将日均收看该体育节目时间不低于40分钟的观众称为“体育迷”,已知“体育迷”中有10名女性.| 非体育迷 | 体育迷 | 合计 | |
| 男 | |||
| 女 | |||
| 合计 |
| P(K2≥k) | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{7}{8}$ | B. | -$\frac{7}{8}$ | C. | $\frac{3}{4}$ | D. | -$\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在三棱柱ABC-A1B1C1中,平面BCC1B1⊥平面ABC,四边形BCC1B1为菱形,点M是棱AC上不同于A,C的点,平面B1BM与棱A1C1交于点N,AB=BC=2,∠ABC=90°,∠BB1C1=60°.
如图,在三棱柱ABC-A1B1C1中,平面BCC1B1⊥平面ABC,四边形BCC1B1为菱形,点M是棱AC上不同于A,C的点,平面B1BM与棱A1C1交于点N,AB=BC=2,∠ABC=90°,∠BB1C1=60°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com