
分析 (1)优先位置优先排列,先排列甲,其余全排列即可,
(2)先排列甲,其余全排列即可,
(3)捆绑法,先排甲、乙、丙三人,再把该三人当成一个整体,再加上另2人,相当于3人的全排列,
(4)插空法,将甲乙丙插入到另外2人所成的空中,
(5)定序法,甲在乙的左边(不一定相邻),占总数的一半,
(6)分类计数法,甲排列当中,甲不排在当中
解答 解:(1)甲固定不动,其余全排列,故有A44=24种;
(2)甲有中间3个位置供选择,故有C31A44=72种;
(3)先排甲、乙、丙三人,再把该三人当成一个整体,再加上另2人,相当于3人的全排列,故有A33A33=36种;
(4)先排甲、乙、丙之外的2人,形成了3个空,将甲、乙、丙三人排这3个空位,故有A22A33=12种;
(5)不考虑限制条件有,甲在乙的左边(不一定相邻),占总数的一半,即$\frac{1}{2}$A55=60种;
(6)第一类,甲排列当中,有A44=24种,第二类,甲不排在当中,有A31A31A33=54种,故有24+54=78种
点评 本题考查排列、组合的应用,注意特殊问题的处理方法,如相邻用捆绑法,不能相邻用插空法.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{2}$ | B. | π | C. | $\frac{π}{3}$ | D. | $\frac{π}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p是假命题 | B. | q是真命题 | C. | p(∧¬q) 是真命题 | D. | (¬p)∧q是真命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
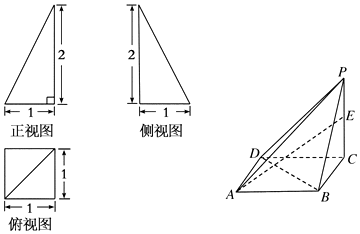
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 10 | B. | -10 | C. | -14 | D. | 无法确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 三棱锥A-BCD中,E是BC的中点,AB=AD,BD⊥DC
三棱锥A-BCD中,E是BC的中点,AB=AD,BD⊥DC查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com