
分析 p真:$\left\{\begin{array}{l}{△>0}\\{m>0}\end{array}\right.$,解得m.q真:可得△=16(m-2)2-16<0,解得m范围.又p和q一真一假即可得出.
解答 解:p:方程x2+mx+1=0有两个不等的负根,则$\left\{\begin{array}{l}{△>0}\\{m>0}\end{array}\right.$,解得m>2.
q:方程4x2+4(m-2)x+1=0无实根.则△=16(m-2)2-16<0,解得1<m<3.
若p和q一真一假,∴$\left\{\begin{array}{l}{m>2}\\{m≤1或m≥3}\end{array}\right.$,或$\left\{\begin{array}{l}{m≤2}\\{1<m<3}\end{array}\right.$,
解得m≥3,或1<m≤2.
∴m的取值范围是(1,2]∪[3,+∞).
点评 本题考查了不等式的解法、方程的实数根与判别式的关系、简易逻辑的判定方法,考查了分类讨论方法、推理能力与计算能力,属于中档题.


 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>b>c | B. | b>c>a | C. | c>b>a | D. | b>a>c |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{2π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
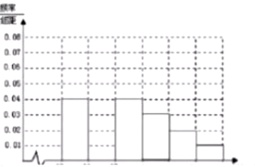 2016年7月23日至24日,本年度第三次二十国集团(G20)财长和央行行长会议在四川省省会成都举行,业内调查机构i Research (艾瑞咨询)在成都市对[25,55]岁的人群中随机抽取n人进行了一次“消费”生活习惯是否符合理财观念的调查,若消费习惯符合理财观念的称为“经纪人”,否则则称为“非经纪人”.则如表统计表和各年龄段人数频率分布直方图
2016年7月23日至24日,本年度第三次二十国集团(G20)财长和央行行长会议在四川省省会成都举行,业内调查机构i Research (艾瑞咨询)在成都市对[25,55]岁的人群中随机抽取n人进行了一次“消费”生活习惯是否符合理财观念的调查,若消费习惯符合理财观念的称为“经纪人”,否则则称为“非经纪人”.则如表统计表和各年龄段人数频率分布直方图| 组数 | 分组 | 经纪人的人数 | 占本组 的频率 |
| 第一组 | [25,30) | 120 | 0.6 |
| 第二组 | [30,35) | 195 | P |
| 第三组 | [35,40) | 100 | 0.5 |
| 第四组 | [40,45) | a | 0.4 |
| 第五组 | [45,50) | 30 | 0.3 |
| 第六组 | [50,55] | 15 | 0.3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com