
分析 (Ⅰ)由已知等式利用特殊角的三角函数值,两角差的正弦函数公式化简可得sinx-cosx=$\frac{7}{5}$,两边平方可得sinxcosx=-$\frac{12}{25}$,结合cos2x=$\frac{7}{25}$,利用二倍角的余弦函数公式可求cosx,sinx的值,
由特殊角的三角函数值,两角和与差的余弦函数公式即可化简求值.
(Ⅱ)由(Ⅰ)cosx,sinx的值,利用同角三角函数基本关系式,倍角公式即可化简求值.
解答 解:(Ⅰ)∵sin(x-$\frac{π}{4}$)=$\frac{{7\sqrt{2}}}{10}$,
⇒$\frac{\sqrt{2}}{2}$(sinx-cosx)=$\frac{{7\sqrt{2}}}{10}$,
⇒sinx-cosx=$\frac{7}{5}$①,
⇒1-2sinxcosx=$\frac{49}{25}$,
⇒sinxcosx=-$\frac{12}{25}$②,
∴由①②可得:cox<0,
又∵cos2x=2cos2x-1=$\frac{7}{25}$,解得:cosx=-$\frac{4}{5}$,由①可得:sinx=$\frac{3}{5}$,
∴$cos({\frac{7π}{12}-x})$
=cos($\frac{π}{3}$+$\frac{π}{4}$-x)
=cos$\frac{π}{3}$cos($\frac{π}{4}$-x)-sin$\frac{π}{3}$sin($\frac{π}{4}$-x)
=$\frac{1}{2}$cos(x-$\frac{π}{4}$)+$\frac{\sqrt{3}}{2}$sin(x-$\frac{π}{4}$)
=$\frac{1}{2}$×$\frac{\sqrt{2}}{2}$(-$\frac{4}{5}$+$\frac{3}{5}$)+$\frac{\sqrt{3}}{2}$×$\frac{{7\sqrt{2}}}{10}$
=$\frac{7\sqrt{6}-\sqrt{2}}{20}$.
(Ⅱ)∵由(Ⅰ)可得:cosx=-$\frac{4}{5}$,sinx=$\frac{3}{5}$,
∴$\frac{{sin2x+2{{sin}^2}x}}{1-tanx}$=$\frac{2sinxcosx+2si{n}^{2}x}{\frac{cosx-sinx}{cosx}}$=-$\frac{24}{175}$.
点评 本题主要考查了特殊角的三角函数值,两角差的正弦函数公式,二倍角的余弦函数公式,两角差的余弦函数公式,同角三角函数基本关系式,倍角公式在三角函数化简求值中的应用,考查了转化思想和计算能力,熟练掌握相关公式的应用是解题的关键,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
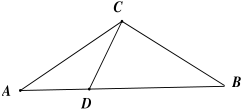 如图,在等腰△ABC中,∠C=120°,DA=DC,过顶点C在∠ACB内部作一条射线CM,与线段AB交于点M,则AM<$\frac{{\sqrt{3}}}{3}$AC的概率为( )
如图,在等腰△ABC中,∠C=120°,DA=DC,过顶点C在∠ACB内部作一条射线CM,与线段AB交于点M,则AM<$\frac{{\sqrt{3}}}{3}$AC的概率为( )| A. | $\frac{{\sqrt{3}}}{3}$ | B. | $\frac{3}{4}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com