
分析 由条件利用正弦函数的图象特征,分类讨论,求得每种情况下正数ω的最小值,从而得出结论.
解答 解:①若只有A、B两点在函数f(x)=sinωx的图象上,
则有sin(ω•$\frac{π}{6}$)=$\frac{\sqrt{3}}{2}$,sin(ω•$\frac{π}{4}$)=1,sinω•$\frac{π}{2}$≠0,
则$\left\{\begin{array}{l}{ω•\frac{π}{6}=2kπ+\frac{π}{3},或ω=2kπ+\frac{2π}{3},k∈Z}\\{ω•\frac{π}{4}=2kπ+\frac{π}{2},k∈Z}\\{ω•\frac{π}{2}≠kπ,k∈Z}\end{array}\right.$,
即 $\left\{\begin{array}{l}{ω=12k+2,或ω=12k+4,k∈Z}\\{ω=8k+2,k∈Z}\\{ω≠2k,k∈Z}\end{array}\right.$,求得ω无解.
②若只有点A($\frac{π}{6}$,$\frac{\sqrt{3}}{2}$),C($\frac{π}{2}$,0)在函数f(x)=sin(ωx)的图象上,
则有sin(ω•$\frac{π}{6}$)=$\frac{\sqrt{3}}{2}$,sin(ω•$\frac{π}{2}$)=0,sin(ω•$\frac{π}{4}$)≠1,
故有 $\left\{\begin{array}{l}{ω•\frac{π}{6}=2kπ+\frac{π}{3},或ω•\frac{π}{6}=2kπ+\frac{2π}{3},k∈Z}\\{ω•\frac{π}{2}=kπ,k∈Z}\\{ω•\frac{π}{4}≠2kπ+\frac{π}{2},k∈Z}\end{array}\right.$,
即 $\left\{\begin{array}{l}{ω=12k+2,或ω=12k+4,k∈Z}\\{ω=2k,k∈Z}\\{ω≠8k+2,k∈Z}\end{array}\right.$,求得ω的最小值为4.
③若只有点B($\frac{π}{4}$,1)、C($\frac{π}{2}$,0)在函数f(x)=sinωx的图象上,
则有sinω•$\frac{π}{6}$≠$\frac{\sqrt{3}}{2}$,sinω$\frac{π}{4}$=1,sinω$\frac{π}{2}$=0,
故有$\left\{\begin{array}{l}{ω•\frac{π}{4}=2kπ+\frac{π}{2},k∈Z}\\{ω•\frac{π}{2}=kπ,k∈Z}\\{ω•\frac{π}{6}≠2kπ+\frac{π}{3},且ω•\frac{π}{6}≠2kπ+\frac{2π}{3},k∈Z}\end{array}\right.$,即 $\left\{\begin{array}{l}{ω=8k+2,k∈Z}\\{ω=2k,k∈Z}\\{ω≠12k+2且ω≠12k+4,k∈Z}\end{array}\right.$,
求得ω的最小正值为10,
综上可得,ω的最小正值为4,
故答案为:4.
点评 本题主要考查正弦函数的图象特征,体现了分类讨论的数学思想,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{4}$ | B. | $\frac{3}{2}$+ln2 | C. | $\frac{5}{2}$+ln2 | D. | 3+ln2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
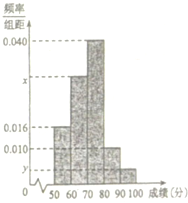 某中学举行了一次“环保知识竞赛”活动,为了了解本次竞赛学生成绩情况,从中抽取了部分学生的分数(得分取正整数,满分为100分)作为样本(样本容量为n)进行统计,按照[50,60),[60,70),[70,80),[80,90),[90,100]的分组作出如图所示的频率分布直方图,但由于不慎丢失了部分数据.已知得分在[50,60)的有8人,在[90,100)的有2人,由此推测频率分布直方图中的x=( )
某中学举行了一次“环保知识竞赛”活动,为了了解本次竞赛学生成绩情况,从中抽取了部分学生的分数(得分取正整数,满分为100分)作为样本(样本容量为n)进行统计,按照[50,60),[60,70),[70,80),[80,90),[90,100]的分组作出如图所示的频率分布直方图,但由于不慎丢失了部分数据.已知得分在[50,60)的有8人,在[90,100)的有2人,由此推测频率分布直方图中的x=( )| A. | 0.04 | B. | 0.03 | C. | 0.02 | D. | 0.01 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | S2>S3>S1 | B. | S1>S3>S2 | C. | S2>S1>S3 | D. | S1>S2>S3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
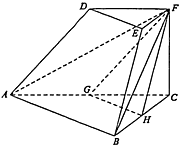 如图,在三棱台DEF-ABC中,已知底面ABC是以AB为斜边的直角三角形,FC⊥底面ABC,AB=2DE,G,H分别为AC,BC的中点.
如图,在三棱台DEF-ABC中,已知底面ABC是以AB为斜边的直角三角形,FC⊥底面ABC,AB=2DE,G,H分别为AC,BC的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com