
| A. | 2 | B. | $2\sqrt{3}$ | C. | 3 | D. | $2\sqrt{5}$ |
分析 可以得到$(\overrightarrow{a}-\overrightarrow{b})^{2}=(\overrightarrow{a}+\overrightarrow{b})^{2}-4\overrightarrow{a}•\overrightarrow{b}$,这样代入$|\overrightarrow{a}+\overrightarrow{b}|=4,\overrightarrow{a}•\overrightarrow{b}=1$即可求出$(\overrightarrow{a}-\overrightarrow{b})^{2}$的值,从而得出$|\overrightarrow{a}-\overrightarrow{b}|$的值.
解答 解:$(\overrightarrow{a}-\overrightarrow{b})^{2}={\overrightarrow{a}}^{2}-2\overrightarrow{a}•\overrightarrow{b}+{\overrightarrow{b}}^{2}$
=${\overrightarrow{a}}^{2}+2\overrightarrow{a}•\overrightarrow{b}+{\overrightarrow{b}}^{2}-4\overrightarrow{a}•\overrightarrow{b}$
=$(\overrightarrow{a}+\overrightarrow{b})^{2}-4\overrightarrow{a}•\overrightarrow{b}$
=16-4
=12;
∴$|\overrightarrow{a}-\overrightarrow{b}|=2\sqrt{3}$.
故选:B.
点评 考查向量数量积的运算及计算公式,以及完全平方公式的运用.


科目:高中数学 来源: 题型:选择题
| A. | (0,+∞) | B. | (-∞,-1) | C. | (-∞,-3) | D. | (0,-3) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
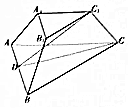 已知三棱台ABC-A1B1C1中,AB=BC=4,AC=2A1C1=2$\sqrt{2}$,AA1=CC1=1,平面AA1B1B⊥平面AA1C1C.
已知三棱台ABC-A1B1C1中,AB=BC=4,AC=2A1C1=2$\sqrt{2}$,AA1=CC1=1,平面AA1B1B⊥平面AA1C1C.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若命题p:?x0∈R,x02-x0+1<0,则¬p:?x∉R,x2-x+1≥0 | |
| B. | 已知相关变量(x,y)满足回归方程$\stackrel{∧}{y}$=2-4x,若变量x增加一个单位,则y平均增加4个单位 | |
| C. | 命题“若圆C:(x-m+1)2+(y-m)2=1与两坐标轴都有公共点,则实数m∈[0,1]为真命题 | |
| D. | 已知随机变量X~N(2,σ2),若P(X<a)=0.32,则P(X>4-a)=0.68 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-3,3] | B. | (-∞,-3]∪[3,+∞) | C. | (-∞,-1]∪[1,+∞) | D. | [-1,1] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
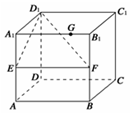 在棱长为1的正方体ABCD-A1B1C1D1中,E、F分别为棱AA1、BB1的中点,G为棱A1B1上的一点,且A1G=λ(0≤λ≤1),则点G到平面D1EF的距离为$\frac{{\sqrt{5}}}{5}$.
在棱长为1的正方体ABCD-A1B1C1D1中,E、F分别为棱AA1、BB1的中点,G为棱A1B1上的一点,且A1G=λ(0≤λ≤1),则点G到平面D1EF的距离为$\frac{{\sqrt{5}}}{5}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com