
���� ��1��{an}��{bn}������������У���4∉A��4∉B��4∉A��B=N*�������жϣ�
��2����an=2n���ɵ�a4=16��a5=32�������¶���ɵ�b16=16+4=20�����õȲ����е����ʽ�����㼴�ɵõ�����ͣ�
��3�����õȲ����е�ͨ�ʽ�����������ڵ���1���ɵ�d=1��2������d=1��2���ͨ�ʽ������¶��壬���ɵõ��������е�ͨ�ʽ��
��� �⣺��1��{an}��{bn}������������У�
���ɣ���an=2n-1��bn=4n-2���ɵ�4∉A��4∉B��
����4∉A��B=N*������{an}��{bn}������������У�
��2����an=2n���ɵ�a4=16��a5=32��
��{an}��{bn}����������У��ɵ�b16=16+4=20��
��������{bn}��ǰ16��ĺ�Ϊ
��1+2+3+��+20��-��2+4+8+16��=$\frac{1+20}{2}$��20-30=180��
��3����{an}Ϊ����Ϊd��dΪ���������ĵȲ�������a16=36����a1+15d=36��
��a1=36-15d��1���ɵ�d=1��2��
��d=1����a1=21��an=n+20��bn=n��1��n��20����
��{an}��{bn}�����������ì�ܣ���ȥ��
��d=2����a1=6��an=2n+4��bn=$\left\{\begin{array}{l}{n��n��5}\\{2n-5��n��5}\end{array}\right.$��
���Ͽɵã�an=2n+4��bn=$\left\{\begin{array}{l}{n��n��5}\\{2n-5��n��5}\end{array}\right.$��
���� ���⿼���¶������������ã�����Ȳ����е�ͨ�ʽ�����ʽ�����ã�������������������������е��⣮


 ����С״Ԫ��������������ϵ�д�
����С״Ԫ��������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����

| A�� | $\frac{n��3n-1��}{2}$ | B�� | $\frac{��3n+2����n+1��}{2}$ | C�� | $\frac{��3n-2����n+1��}{2}$ | D�� | $\frac{��3n+2����n-1��}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
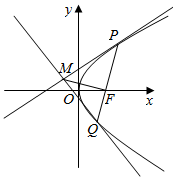 ��ͼ��ʾ��ֱ��l����������y2=2px��p��0���Ľ���F�����������߽��ڵ�P��Q���㣬��P��Q�ֱ��������ߵ����߽���M�����|PF|=a��|QF|=b����|MF|��ֵΪ��������
��ͼ��ʾ��ֱ��l����������y2=2px��p��0���Ľ���F�����������߽��ڵ�P��Q���㣬��P��Q�ֱ��������ߵ����߽���M�����|PF|=a��|QF|=b����|MF|��ֵΪ��������| A�� | a+b | B�� | $\frac{1}{2}��a+b��$ | C�� | ab | D�� | $\sqrt{ab}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{{3\sqrt{10}}}{10}$ | B�� | $\frac{{\sqrt{10}}}{10}$ | C�� | $\frac{{\sqrt{19}}}{19}$ | D�� | $\frac{{\sqrt{30}}}{30}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com