
| A. | 只有一个 | B. | 有二个 | C. | 有四个 | D. | 有无穷多个 |
分析 先把ABCD看成是平面图形,过B作BE垂直AC,过D作DF垂直AC,运用勾股定理,可得E,F重合,再将图形沿AC或BD折起,便是空间图形,运用线面垂直的判定和性质,得AC⊥BD,再由向量数量积的性质,即可得到答案.
解答 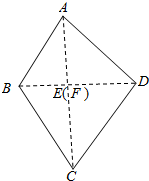 解:由|$\overline{AB}$|=3,|$\overrightarrow{BC}$|=7,|$\overrightarrow{CD}$|=11,|$\overrightarrow{DA}$|=9,
解:由|$\overline{AB}$|=3,|$\overrightarrow{BC}$|=7,|$\overrightarrow{CD}$|=11,|$\overrightarrow{DA}$|=9,
知AB2+CD2=BC2+DA2=130,
BC2-AB2=CD2-DA2;
先把ABCD看成是平面图形,
过B作BE垂直AC,过D作DF垂直AC,
则AB2=AE2+BE2,BC2=CE2+BE2,
则BC2-AB2=CE2-AE2.
同理CD2-DA2=CF2-AF2,即CF2-AF2=CE2-AE2,
又因为A,E,F,C在一条直线上,
所以满足条件的只能是E,F重合,即有AC垂直BD,
再将图形沿AC或BD折起,便是空间图形;
由AC⊥BE,AC⊥DE,即有AC⊥平面BDE,则AC⊥BD,
即$\overrightarrow{AC}$•$\overrightarrow{BD}$=0,所以$\overrightarrow{AC}$•$\overrightarrow{BD}$的取值只有一个.
故选:A.
点评 本题考查了空间中直线和平面的位置关系,以及向量的数量积的应用问题,也考查了空间想象能力,是中档题目.


科目:高中数学 来源: 题型:选择题
| A. | {x|-1<x<3} | B. | {x|0≤x≤2} | C. | {0,1,2} | D. | {0,1,2,3} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(-\sqrt{2},-\frac{{\sqrt{6}}}{2})∪(\frac{{\sqrt{6}}}{2},\sqrt{2})$ | B. | $[-\sqrt{2},-\frac{{\sqrt{6}}}{2})∪(\frac{{\sqrt{6}}}{2},\sqrt{2}]$ | C. | $[-\sqrt{2},-\frac{{\sqrt{6}}}{2}]∪[\frac{{\sqrt{6}}}{2},\sqrt{2}]$ | D. | $[\frac{{\sqrt{6}}}{2},\sqrt{2}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
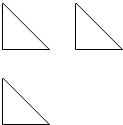 某几何体的三视图如图所示(均为直角边长为2的等腰直角三角形),则该几何体的表面积为( )
某几何体的三视图如图所示(均为直角边长为2的等腰直角三角形),则该几何体的表面积为( )| A. | 4+4$\sqrt{2}$ | B. | 4+4$\sqrt{3}$ | C. | 6+2$\sqrt{3}$ | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x轴对称 | B. | y轴对称 | C. | 原点对称 | D. | 直线y=x对称 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
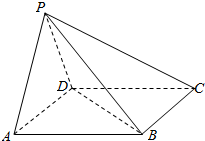 如图,四棱锥P-ABCD的底面ABCD是矩形,侧面PAD是等腰三角形∠APD=90°,且平面PAD⊥平面ABCD
如图,四棱锥P-ABCD的底面ABCD是矩形,侧面PAD是等腰三角形∠APD=90°,且平面PAD⊥平面ABCD查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com