Question

6．定义代数运算a?b=$\sqrt{1-\frac{1}{2}ab}$-ka-2，则当方程x?x=0有两个不同解时，实数k的取值范围是（　　）

• A． $（-\sqrt{2}，-\frac{{\sqrt{6}}}{2}）∪（\frac{{\sqrt{6}}}{2}，\sqrt{2}）$
• B． $[-\sqrt{2}，-\frac{{\sqrt{6}}}{2}）∪（\frac{{\sqrt{6}}}{2}，\sqrt{2}]$
• C． $[-\sqrt{2}，-\frac{{\sqrt{6}}}{2}]∪[\frac{{\sqrt{6}}}{2}，\sqrt{2}]$
• D． $[\frac{{\sqrt{6}}}{2}，\sqrt{2}]$

Answer 1

分析 根据定义运算求出x?x=0的表达式，利用函数与方程之间的关系转化为两个函数的交点关系，结合直线和椭圆的位置关系进行求解即可．

解答 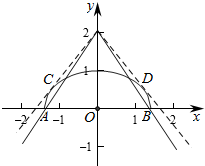解：∵a?b=$\sqrt{1-\frac{1}{2}ab}$-ka-2，
∴x?x=$\sqrt{1-\frac{1}{2}{x}^{2}}$-kx-2，
由x?x=$\sqrt{1-\frac{1}{2}{x}^{2}}$-kx-2=0得$\sqrt{1-\frac{1}{2}{x}^{2}}$=kx+2，
设y=$\sqrt{1-\frac{1}{2}{x}^{2}}$和y=kx+2，
作出两个函数的图象如图：
由y=$\sqrt{1-\frac{1}{2}{x}^{2}}$=0得x²=2，即x=$\sqrt{2}$或x=-$\sqrt{2}$，
当直线经过点A（-$\sqrt{2}$，0），B（$\sqrt{2}$，0）时，直线和椭圆有两个交点，
此时由$\sqrt{2}$k+2=0得k=-$\frac{2}{\sqrt{2}}$=-$\sqrt{2}$，
由-$\sqrt{2}$k+2=0得k=$\frac{2}{\sqrt{2}}$=$\sqrt{2}$，
当直线与椭圆相切时得1-$\frac{1}{2}$x²=（kx+2）²，
即（2k²+1）x²+8kx+6=0，
由判别式△=0得△=64k²-24（2k²+1）=0
即16k²-24=0，
则k²=$\frac{3}{2}$得k=$\frac{\sqrt{6}}{2}$或-$\frac{\sqrt{6}}{2}$，
则要使方程x?x=0有两个不同解，则-$\sqrt{2}$≤k＜-$\frac{\sqrt{6}}{2}$或$\frac{\sqrt{6}}{2}$＜k≤$\sqrt{2}$，
即实数k的取值范围是$[-\sqrt{2}，-\frac{{\sqrt{6}}}{2}）∪（\frac{{\sqrt{6}}}{2}，\sqrt{2}]$，
故选：B．

点评 本题主要考查函数与方程的应用，利用定义求出方程，利用函数与方程的关系转化为两个函数的交点个数问题，结合数形结合进行求解是解决本题的关键．