
分析 利用空间中线线、线面、面面间的位置关系求解.
解答 解:在①中:∵“直线a,b没有公共点”⇒“直线a,b为异面直线或平行线”,
“直线a,b为异面直线”⇒“直线a,b没有公共点”,
∴“直线a,b没有公共点”是“直线a,b为异面直线”的必要不充分条件,故①正确;
在②中,“直线a,b和平面α所成的角相等”⇒“直线a,b平行、相交或异面”,
“直线a,b平行”⇒“直线a,b和平面α所成的角相等”,
∴“直线a,b和平面α所成的角相等”是“直线a,b平行”的必要充分不条件,故②错误;
③“直线l平行于两个相交平面α,β”是“直线l与平面α,β的交线平行”的必要不充分条件,故③错误;
④“直线l与平面α内无数条直线都垂直”⇒“直线l与平面α相交、平行或直线在平面内”,
“直线l⊥平面α”⇒“直线l与平面α内无数条直线都垂直”,
∴“直线l与平面α内无数条直线都垂直”是“直线l⊥平面α”的必要不充分条件,故④正确.
故答案为:①④.
点评 本题考查命题真假的判断,是中档题,解题时要认真审题,注意空间中线线、线面、面面间的位置关系的合理运用.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(-\sqrt{2},-\frac{{\sqrt{6}}}{2})∪(\frac{{\sqrt{6}}}{2},\sqrt{2})$ | B. | $[-\sqrt{2},-\frac{{\sqrt{6}}}{2})∪(\frac{{\sqrt{6}}}{2},\sqrt{2}]$ | C. | $[-\sqrt{2},-\frac{{\sqrt{6}}}{2}]∪[\frac{{\sqrt{6}}}{2},\sqrt{2}]$ | D. | $[\frac{{\sqrt{6}}}{2},\sqrt{2}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x轴对称 | B. | y轴对称 | C. | 原点对称 | D. | 直线y=x对称 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
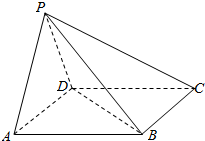 如图,四棱锥P-ABCD的底面ABCD是矩形,侧面PAD是等腰三角形∠APD=90°,且平面PAD⊥平面ABCD
如图,四棱锥P-ABCD的底面ABCD是矩形,侧面PAD是等腰三角形∠APD=90°,且平面PAD⊥平面ABCD查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com