
【题目】[选修4-4:坐标系与参数方程]
在平面直角坐标系中,曲线C1: ![]() (a为参数)经过伸缩变换
(a为参数)经过伸缩变换 ![]() 后的曲线为C2 , 以坐标原点为极点,x轴正半轴为极轴建立极坐标系.
后的曲线为C2 , 以坐标原点为极点,x轴正半轴为极轴建立极坐标系.
(Ⅰ)求C2的极坐标方程;
(Ⅱ)设曲线C3的极坐标方程为ρsin( ![]() ﹣θ)=1,且曲线C3与曲线C2相交于P,Q两点,求|PQ|的值.
﹣θ)=1,且曲线C3与曲线C2相交于P,Q两点,求|PQ|的值.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】我国南北朝时代的数学家祖暅提出体积的计算原理(祖暅原理):“幂势既同,则积不容 异”.“势’’即是高,“幂”是面积.意思是:如果两等高的几何体在同高处截得两几何体的截面积恒等,那么这两个几何体的体积相等,类比祖暅原理,如图所示,在平面直角坐标系中,图1是一个形状不规则的封闭图形,图2是一个上底为l的梯形,且当实数t取[0,3]上的任意值时,直线y=t被图l和图2所截得的两线段长始终相等,则图l的面积为 . 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数y=f(x)与y=F(x)的图象关于y轴对称,当函数y=f(x)和y=F(x)在区间[a,b]同时递增或同时递减时,把区间[a,b]叫做函数y=f(x)的“不动区间”.若区间[1,2]为函数f(x)=|2x﹣t|的“不动区间”,则实数t的取值范围是( )
A.(0,2]
B.[ ![]() ,+∞)
,+∞)
C.[ ![]() ,2]
,2]
D.[ ![]() ,2]∪[4,+∞)
,2]∪[4,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (k
(k![]() R),且满足f(﹣1)=f(1).
R),且满足f(﹣1)=f(1).
(1)求k的值;
(2)若函数y=f(x)的图象与直线![]() 没有交点,求a的取值范围;
没有交点,求a的取值范围;
(3)若函数![]() ,x
,x![]() [0,log23],是否存在实数m使得h(x)最小值为0,若存在,求出m的值;若不存在,请说明理由.
[0,log23],是否存在实数m使得h(x)最小值为0,若存在,求出m的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,抛物线y2=4x的一条弦AB经过焦点F,取线段OB的中点D,延长OA至点C,使|OA|=|AC|,过点C,D作y轴的垂线,垂足分别为E,G,则|EG|的最小值为 . 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆锥母线长为5,底面圆半径长为4,点M是母线PA的中点,AB是底面圆的直径,点C是弧AB的中点; 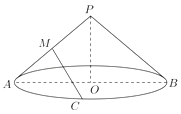
(1)求三棱锥P﹣ACO的体积;
(2)求异面直线MC与PO所成的角.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com