
【题目】由直线x+2y![]() 7=0上一点P引圆x2+y2
7=0上一点P引圆x2+y2![]() 2x+4y+2=0的一条切线,切点为A,则|PA|的最小值为__________
2x+4y+2=0的一条切线,切点为A,则|PA|的最小值为__________
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,过其右焦点F且与x轴垂直的直线交椭圆C于P,Q两点,椭圆C的右顶点为R,且满足
,过其右焦点F且与x轴垂直的直线交椭圆C于P,Q两点,椭圆C的右顶点为R,且满足![]() .
.
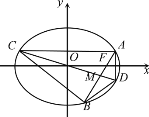
(1)求椭圆C的方程;
(2)若斜率为k(其中![]() )的直线l过点F,且与椭圆交于点A,B,弦AB的中点为M,直线OM与椭圆交于点C,D,求四边形ACBD面积
)的直线l过点F,且与椭圆交于点A,B,弦AB的中点为M,直线OM与椭圆交于点C,D,求四边形ACBD面积![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】闽越水镇是闽侯县打造闽都水乡文化特色小镇核心区,该小镇有一块1800平方米的矩形地块,开发商准备在中间挖出三个矩形池塘养闽侯特色金鱼,挖出的泥土堆在池塘四周形成基围(阴影部分所示)种植柳树,形成柳中观鱼特色景观.假设池塘周围的基围宽均为2米,如图,设池塘所占的总面积为![]() 平方米.
平方米.

(1)试用![]() 表示a及
表示a及![]() ;
;
(2)当![]() 取何值时,才能使得
取何值时,才能使得![]() 最大?并求出
最大?并求出![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=8lnx+15x﹣x2 , 数列{an}满足an=f(n),n∈N+ , 数列{an}的前n项和Sn最大时,n=( )
A.15
B.16
C.17
D.18
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)= ![]() ,若方程f(f(x))=a(a>0)恰有两个不相等的实根x1 , x2 , 则e
,若方程f(f(x))=a(a>0)恰有两个不相等的实根x1 , x2 , 则e ![]() e
e ![]() 的最大值为( )
的最大值为( )
A.![]()
B.2(ln2﹣1)
C.![]()
D.ln2﹣1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C经过原点O(0,0)且与直线y=2x﹣8相切于点P(4,0).
(1)求圆C的方程;
(2)已知直线l经过点(4, 5),且与圆C相交于M,N两点,若|MN|=2,求出直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-5:不等式选讲]
设函数f(x)=|2x+2|﹣|x﹣2|.
(Ⅰ)求不等式f(x)>2的解集;
(Ⅱ)若x∈R,f(x)≥t2﹣ ![]() t恒成立,求实数t的取值范围.
t恒成立,求实数t的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-4:坐标系与参数方程]
在平面直角坐标系中,曲线C1: ![]() (a为参数)经过伸缩变换
(a为参数)经过伸缩变换 ![]() 后的曲线为C2 , 以坐标原点为极点,x轴正半轴为极轴建立极坐标系.
后的曲线为C2 , 以坐标原点为极点,x轴正半轴为极轴建立极坐标系.
(Ⅰ)求C2的极坐标方程;
(Ⅱ)设曲线C3的极坐标方程为ρsin( ![]() ﹣θ)=1,且曲线C3与曲线C2相交于P,Q两点,求|PQ|的值.
﹣θ)=1,且曲线C3与曲线C2相交于P,Q两点,求|PQ|的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com