
【题目】[选修4-5:不等式选讲]
设函数f(x)=|2x+2|﹣|x﹣2|.
(Ⅰ)求不等式f(x)>2的解集;
(Ⅱ)若x∈R,f(x)≥t2﹣ ![]() t恒成立,求实数t的取值范围.
t恒成立,求实数t的取值范围.
【答案】解:(Ⅰ)函数f(x)=|2x+2|﹣|x﹣2|= 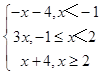 , 当x<﹣1时,不等式即﹣x﹣4>2,求得x<﹣6,∴x<﹣6.
, 当x<﹣1时,不等式即﹣x﹣4>2,求得x<﹣6,∴x<﹣6.
当﹣1≤x<2时,不等式即3x>2,求得x> ![]() ,∴
,∴ ![]() <x<2.
<x<2.
当x≥2时,不等式即x+4>2,求得x>﹣2,∴x≥2.
综上所述,不等式的解集为{x|x> ![]() 或x<﹣6}.
或x<﹣6}.
(Ⅱ)由以上可得f(x)的最小值为f(﹣1)=﹣3,若x∈R,f(x)≥t2﹣ ![]() t恒成立,
t恒成立,
只要﹣3≥t2﹣ ![]() t,即2t2﹣7t+6≤0,求得
t,即2t2﹣7t+6≤0,求得 ![]() ≤t≤2.
≤t≤2.
【解析】(Ⅰ)根据函数f(x)= 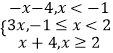 ,分类讨论,求得f(x)>2的解集.(Ⅱ)由f(x)的解析式求得f(x)的最小值为f(﹣1)=﹣3,再根据f(﹣1)≥t2﹣
,分类讨论,求得f(x)>2的解集.(Ⅱ)由f(x)的解析式求得f(x)的最小值为f(﹣1)=﹣3,再根据f(﹣1)≥t2﹣ ![]() ,求得实数t的取值范围.
,求得实数t的取值范围.
【考点精析】关于本题考查的绝对值不等式的解法,需要了解含绝对值不等式的解法:定义法、平方法、同解变形法,其同解定理有;规律:关键是去掉绝对值的符号才能得出正确答案.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2-x+c定义在区间[0,1]上,x1,x2∈
[0,1],且x1≠x2,求证:
(1)f(0)=f(1);
(2)|f(x2)-f(x1)|<|x1-x2|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=sin(ωx+ ![]() )(ω>0)的图象与x轴的交点横坐标构成一个公差为
)(ω>0)的图象与x轴的交点横坐标构成一个公差为 ![]() 的等差数列,要得到g(x)=cos(ωx+
的等差数列,要得到g(x)=cos(ωx+ ![]() )的图象,可将f(x)的图象( )
)的图象,可将f(x)的图象( )
A.向右平移 ![]() 个单位
个单位
B.向左平移 ![]() 个单位
个单位
C.向左平移 ![]() 个单位
个单位
D.向右平移 ![]() 个单位
个单位
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P-ABCD中,侧面PAD是边长为2的等边三角形且垂直于底![]() ,
, ![]()
![]() 是
是![]() 的中点。
的中点。
(1)证明:直线![]() 平面
平面![]() ;
;
(2)点![]() 在棱
在棱![]() 上,且直线
上,且直线![]() 与底面
与底面![]() 所成角为
所成角为![]() ,求二面角
,求二面角![]() 的余弦值。
的余弦值。

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 分别是双曲线E:
分别是双曲线E: ![]()
![]() 的左、右焦点,P是双曲线上一点,
的左、右焦点,P是双曲线上一点, ![]() 到左顶点的距离等于它到渐近线距离的2倍,(1)求双曲线的渐近线方程;(2)当
到左顶点的距离等于它到渐近线距离的2倍,(1)求双曲线的渐近线方程;(2)当![]() 时,
时, ![]() 的面积为
的面积为![]() ,求此双曲线的方程。
,求此双曲线的方程。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国南北朝时代的数学家祖暅提出体积的计算原理(祖暅原理):“幂势既同,则积不容 异”.“势’’即是高,“幂”是面积.意思是:如果两等高的几何体在同高处截得两几何体的截面积恒等,那么这两个几何体的体积相等,类比祖暅原理,如图所示,在平面直角坐标系中,图1是一个形状不规则的封闭图形,图2是一个上底为l的梯形,且当实数t取[0,3]上的任意值时,直线y=t被图l和图2所截得的两线段长始终相等,则图l的面积为 . 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,抛物线y2=4x的一条弦AB经过焦点F,取线段OB的中点D,延长OA至点C,使|OA|=|AC|,过点C,D作y轴的垂线,垂足分别为E,G,则|EG|的最小值为 . 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com