Question

已知函数f(x)=sinωx·cosωx-cos²ωx+(ω∈R,x∈R)的最小正周期为π,且图象关于直线x=对称.

（1）求f(x)的解析式；

（2）若函数y=1-f(x)的图象与直线y=a在［0,］上只有一个交点，求实数a的取值范围.

Answer 1

解：（1）∵f(x)=sinωx·cosωx-cos²ωx+=sin2ωx-(1+cos2ωx)+=sin(2ωx-)+1,由f(x)的周期为π,∴=πω=±1,∴f(x)=sin(±2x-)+1.

①当ω=1时，f(x)=sin(2x-)+1,

∵f()=sin+1不是最大或最小值，其图象不关于x=对称，舍去.

②当ω=-1时，f(x)=-sin(2x+)+1,

∵f()=-sin+1=0是最小值，其图象关于x=对称.故f(x)=1-sin(2x+)为所求解析式.

（2）∵y=1-f(x)=sin(2x+),在同一坐标系中作出y=sin(2x+)和y=a的图象.

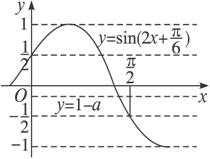
由上图可知，直线y=a在a∈［-,)或a=1时，两曲线只有一个交点，∴a∈［-,）或a=1.