Question

【题目】对某个品牌的U盘进行寿命追踪调查，所得情况如下面频率分布直方图所示．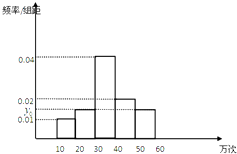
（1）图中纵坐标y0处刻度不清，根据图表所提供的数据还原y0；
（2）根据图表的数据按分层抽样，抽取20个U盘，寿命为1030万次之间的应抽取几个；
（3）从（2）中抽出的寿命落在1030万次之间的元件中任取2个元件，求事件“恰好有一个寿命为1020万次，一个寿命为2030万次”的概率．

Answer 1

【答案】
（1）解：∵0.01×10+20y0+0.02×10+0.04×10=1，∴y0=0.015
（2）解：10～30万次之间的U盘所占频率为0.01×10+0.015×10=0.25，

设10～30万次之间的U盘应抽取x个， ，∴x=5

（3）解：10～20万次应抽取20×10×0.01=2个，设为a1，a2，

20～30万次应抽取20×10×0.015=3个，

设为b1，b2，b3，寿命落在1030万次之间的元件中任取2个元件，一切可能结果组成的基本事件空间为

“抽取的两个U盘恰好有一个寿命为1020万次，一个寿命为2030万次”为事件A，则A={（a1，b1），（a1，b2），（a2，b1），（a2，b2），（a3，b1），（a3，b2）}，

则对应的概率

【解析】（1）图根据频率分布直方图进行求解；（2）利用分层抽样的定义建立比例关系即可得到结论．（3）利用列举法进行求解．
【考点精析】本题主要考查了分层抽样的相关知识点，需要掌握先将总体中的所有单位按照某种特征或标志（性别、年龄等）划分成若干类型或层次，然后再在各个类型或层次中采用简单随机抽样或系用抽样的办法抽取一个子样本，最后，将这些子样本合起来构成总体的样本才能正确解答此题．