
【题目】高一某班级在学校数学嘉年华活动中推出了一款数学游戏,受到大家的一致追捧.游戏规则如下:游戏参与者连续抛掷一颗质地均匀的骰子,记第i次得到的点数为![]() ,若存在正整数n,使得
,若存在正整数n,使得![]() ,则称为游戏参与者的幸运数字。
,则称为游戏参与者的幸运数字。
(I)求游戏参与者的幸运数字为1的概率;
(Ⅱ)求游戏参与者的幸运数字为2的概率,
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】在四边形ABCD中,对角线AC,BD垂直相交于点O,且OA=OB=OD=4,OC=3. 将△BCD沿BD折到△BED的位置,使得二面角E﹣BD﹣A的大小为90°(如图).已知Q为EO的中点,点P在线段AB上,且 ![]() .
.
(Ⅰ)证明:直线PQ∥平面ADE;
(Ⅱ)求直线BD与平面ADE所成角θ的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个口袋中装有大小、材质都相同的![]() 个红球,
个红球,![]() 个黑球和
个黑球和![]() 个白球,从口袋中一次摸出一个球,连续摸球两次.
个白球,从口袋中一次摸出一个球,连续摸球两次.
(![]() )如果摸出后不放回,求第一次摸出黑球,第二次摸出白球的概率;
)如果摸出后不放回,求第一次摸出黑球,第二次摸出白球的概率;
(![]() )如果摸出后放回,求恰有一次摸到黑球的概率.
)如果摸出后放回,求恰有一次摸到黑球的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某校期中考试数学试卷中,抽取样本,考察成绩分布,将样本分成5组,绘成频率分布直方图,图中各小组的长方形面积之比从左至右依次为1:3:6:4:2,第一组的频数是4.

(1)求样本容量及各组对应的频率;
(2)根据频率分布直方图估计成绩的平均分和中位数(结果保留两位小数).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,以x轴正半轴为始边作锐角α,其终边与单位圆交于点A.以OA为始边作锐角β,其终边与单位圆交于点B,AB= ![]() .
. 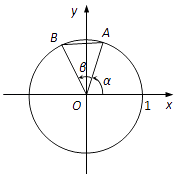
(1)求cosβ的值;
(2)若点A的横坐标为 ![]() ,求点B的坐标.
,求点B的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax2﹣x﹣lnx,a∈R.
(1)当 ![]() 时,求函数f(x)的最小值;
时,求函数f(x)的最小值;
(2)若﹣1≤a≤0,证明:函数f(x)有且只有一个零点;
(3)若函数f(x)有两个零点,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
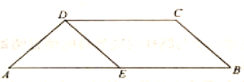
【题目】如图所示,在等腰梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 为
为![]() 的中点.将
的中点.将![]() 沿
沿![]() 折起,使点
折起,使点![]() 到达
到达![]() 的位置,得到如图所示的四棱锥
的位置,得到如图所示的四棱锥![]() ,点
,点![]() 为棱
为棱![]() 的中点.
的中点.
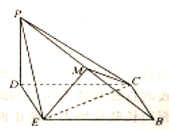
(1)求证:![]() 平面
平面![]() ;
;
(2)若平面![]() 平面
平面![]() ,求三棱锥
,求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的首项为1,且
的首项为1,且![]() ,数列
,数列![]() 满足
满足![]() ,
,![]() ,对任意
,对任意![]() ,都有
,都有![]() .
.
(1)求数列![]() 、
、![]() 的通项公式;
的通项公式;
(2)令![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() .若对任意的
.若对任意的![]() ,不等式
,不等式![]() 恒成立,试求实数
恒成立,试求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】执行如图所示的程序框图后,记“输出![]() 是好点”为事件A.
是好点”为事件A.

(1)若![]() 为区间
为区间![]() 内的整数值随机数,
内的整数值随机数,![]() 为区间
为区间![]() 内的整数值随机数,求事件A发生的概率;
内的整数值随机数,求事件A发生的概率;
(2)若![]() 为区间
为区间![]() 内的均匀随机数,
内的均匀随机数,![]() 为区间
为区间![]() 内的均匀随机数,求事件A发生的概率.
内的均匀随机数,求事件A发生的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com