
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是平行四边形,
是平行四边形, ![]() .
.

(1)求证:平面![]() 平面
平面![]() ;
;
(2)若![]() ,试判断棱
,试判断棱![]() 上是否存在与点
上是否存在与点![]() 不重合的点
不重合的点![]() ,使得直线
,使得直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,若存在,求出
,若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】(1)见解析(2) 棱![]() 上不存在与点
上不存在与点![]() 不重合的点
不重合的点![]() ,使得直线
,使得直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.
【解析】试题分析:(1)第(1)问,把平面![]() 平面
平面![]() 平面
平面![]() (2)第(2)问,先利用向量法得到直线
(2)第(2)问,先利用向量法得到直线![]() 与平面
与平面![]() 所成角的方程,再探究方程的解的情况,从而得到解答.
所成角的方程,再探究方程的解的情况,从而得到解答.
试题解析:
(1)因为四边形![]() 是平行四边形,
是平行四边形, ![]() ,所以
,所以![]() ,
,
又![]() ,所以
,所以![]() ,所以
,所以![]() ,
,
又![]() ,且
,且![]() ,所以
,所以![]() 平面
平面![]() ,
,
因为![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() .
.
(2)由(1)知![]() 平面
平面![]() ,
,
如图,分别以![]() 所在直线为
所在直线为![]() 轴、
轴、![]() 轴,平面
轴,平面![]() 内过点
内过点![]() 且与直线
且与直线![]() 垂直的直线为
垂直的直线为![]() 轴,建立空间直角坐标系
轴,建立空间直角坐标系![]() ,
,
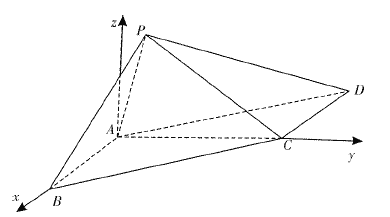
则![]()
由![]() ,
, ![]() ,可得
,可得![]() ,
,
所以![]() ,
,
假设棱![]() 上存在点
上存在点![]() ,使得直线
,使得直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,
,
设![]() ,
,
则![]() ,
, ![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,
,
则![]() ,即
,即![]() ,令
,令![]() ,可得
,可得![]() ,
,
所以平面![]() 的一个法向量为
的一个法向量为![]() ,
,
设直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,则
,则
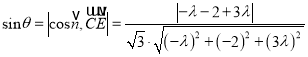
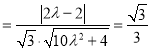 ,
,
整理得![]() ,因为
,因为![]() ,所以
,所以![]() ,故
,故![]() 无解,
无解,
所以棱![]() 上不存在与点
上不存在与点![]() 不重合的点
不重合的点![]() ,使得直线
,使得直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.


 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:高中数学 来源: 题型:
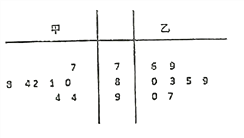
【题目】为了调查观众对电视剧《风筝》的喜爱程度,某电视台举办了一次现场调查活动.在参加此活动的甲、乙两地观众中,各随机抽取了8名观众对该电视剧评分做调查(满分100分),被抽取的观众的评分结果如图所示
(Ⅰ)计算:①甲地被抽取的观众评分的中位数;
②乙地被抽取的观众评分的极差;
(Ⅱ)用频率估计概率,若从乙地的所有观众中再随机抽取4人进行评分调查,记抽取的4人评分不低于90分的人数为![]() ,求
,求![]() 的分布列与期望;
的分布列与期望;
(Ⅲ)从甲、乙两地分别抽取的8名观众中各抽取一人,在已知两人中至少一人评分不低于90分的条件下,求乙地被抽取的观众评分低于90分的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 和
和![]() 满足
满足![]() ,
,![]() ,
,![]() ,
,![]() .
.
(1)证明:![]() 是等比数列,
是等比数列,![]() 是等差数列;
是等差数列;
(2)求![]() 和
和![]() 的通项公式;
的通项公式;
(3)令 ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]() 的通项公式,并求数列
的通项公式,并求数列![]() 的最大值、最小值,并指出分别是第几项.
的最大值、最小值,并指出分别是第几项.
查看答案和解析>>
科目:高中数学 来源: 题型:
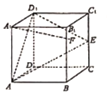
【题目】如图所示,在正方体![]() 中,E是棱
中,E是棱![]() 的中点,F是侧面内
的中点,F是侧面内![]() 的动点,且
的动点,且![]() 平面
平面![]() ,给出下列命题:
,给出下列命题:
![]() 点F的轨迹是一条线段;
点F的轨迹是一条线段;![]() 与
与![]() 不可能平行;
不可能平行;![]() 与BE是异面直线;
与BE是异面直线;![]() 平面
平面![]() 不可能与平面
不可能与平面![]() 平行.
平行.
其中正确的个数是![]()
![]()
A. 0B. 1C. 2D. 3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,以
中,以![]() 轴为始边做两个锐角
轴为始边做两个锐角![]() ,它们的终边分别与单位圆相交于A,B两点,已知A,B的横坐标分别为
,它们的终边分别与单位圆相交于A,B两点,已知A,B的横坐标分别为![]()

(1)求![]() 的值; (2)求
的值; (2)求![]() 的值。
的值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com