
【题目】已知数列![]() 满足
满足![]() ,函数
,函数![]() 是定义在
是定义在![]() 上的奇函数,且满足
上的奇函数,且满足![]() .
.
(Ⅰ)确定![]() 与
与![]() 的关系式,并求
的关系式,并求![]() 的解析式.
的解析式.
(Ⅱ)若数列![]() 的前
的前![]() 项和为
项和为![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() ,是否存在实数
,是否存在实数![]() ,使得对于任意的
,使得对于任意的![]() ,都有
,都有![]() 恒成立?若存在,求出
恒成立?若存在,求出![]() 的最大值.
的最大值.
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其中
,其中![]() 是自然对数的底数,
是自然对数的底数,![]() .
.
(1) 若![]() 是函数
是函数![]() 的导函数,当
的导函数,当![]() 时,解关于
时,解关于![]() 的不等式
的不等式![]() ;
;
(2) 若![]() 在
在![]() 上是单调增函数,求
上是单调增函数,求![]() 的取值范围;
的取值范围;
(3) 当![]() 时,求整数
时,求整数![]() 的所有值,使方程
的所有值,使方程![]() 在
在![]() 上有解.
上有解.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】过椭圆E:![]() 1(a>b>0)上一动点P向圆O:x2+y2=b2引两条切线PA,PB,切点分别是A,B.直线AB分别与x轴,y轴交于点M,N(O为坐标原点).
1(a>b>0)上一动点P向圆O:x2+y2=b2引两条切线PA,PB,切点分别是A,B.直线AB分别与x轴,y轴交于点M,N(O为坐标原点).

(1)若在椭圆E上存在点P,满足PA⊥PB,求椭圆E的离心率的取值范围;
(2)求证:在椭圆E内,存在一点C满足|CO|=|CA|=|CP|=|CB|;
(3)若椭圆E的短轴长为2,△MON面积的最小值为![]() ,求椭圆E的方程.
,求椭圆E的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数![]() 的图象向左平移
的图象向左平移![]() 个单位,然后纵坐标不变,横坐标变为原来的
个单位,然后纵坐标不变,横坐标变为原来的![]() 倍,得到
倍,得到![]() 的图象,下面四个结论正确的是( )
的图象,下面四个结论正确的是( )
A. 函数![]() 在区间
在区间![]() 上为增函数
上为增函数
B. 将函数![]() 的图象向右平移
的图象向右平移![]() 个单位后得到的图象关于原点对称
个单位后得到的图象关于原点对称
C. 点![]() 是函数
是函数![]() 图象的一个对称中心
图象的一个对称中心
D. 函数![]() 在
在![]() 上的最大值为
上的最大值为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】又到了品尝小龙虾的季节,小龙虾近几年来被称作是“国民宵夜”风靡国内外.在巨大的需求市场下,湖北的小龙虾产量占据了全国的半壁江山,湖北某地区近几年的小龙虾产量统计如下表:
年份 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
年份代码 | 1 | 2 | 3 | 4 | 5 | 6 |
年产量 | 6.6 | 6.9 | 7.4 | 7.7 | 8 | 8.4 |
(1)根据表中数据,建立![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)根据线性回归方程预测2019年该地区农产品的年产量.
附:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: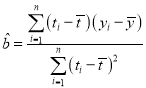 ,
,![]() .(参考数据:
.(参考数据:![]() ,计算结果保留小数点后两位).
,计算结果保留小数点后两位).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】汕尾市基础教育处为调查在校中学生每天放学后的自学时间情况,在本市的所有中学生中随机抽取了120名学生进行调查,现将日均自学时间小于1小时的学生称为“自学不足”者![]() 根据调查结果统计后,得到如下
根据调查结果统计后,得到如下![]() 列联表,已知在调查对象中随机抽取1人,为“自学不足”的概率为
列联表,已知在调查对象中随机抽取1人,为“自学不足”的概率为![]() .
.
非自学不足 | 自学不足 | 合计 | |
配有智能手机 | 30 | ||
没有智能手机 | 10 | ||
合计 |
![]() 请完成上面的列联表;
请完成上面的列联表;
![]() 根据列联表的数据,能否有
根据列联表的数据,能否有![]() 的把握认为“自学不足”与“配有智能手机”有关?
的把握认为“自学不足”与“配有智能手机”有关?
附表及公式: ![]() ,其中
,其中![]()
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线方程为y2=-4x,直线l的方程为2x+y-4=0,在抛物线上有一动点A,点A到y轴的距离为m,到直线l的距离为n,则m+n的最小值为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com