
【题目】已知函数![]()
(1)求函数![]() 的单调区间;
的单调区间;
(2)当![]() 时,判断函数
时,判断函数![]() 在区间
在区间![]() 的零点个数.
的零点个数.
【答案】(1)见解析(2) 当![]() 时,有一个零点为
时,有一个零点为![]() ;当
;当![]() 时,没有零点;当
时,没有零点;当![]() 时,有两个零点.
时,有两个零点.
【解析】试题分析:
(1)由函数的解析式可得![]() ,分类讨论:
,分类讨论:
①当![]() 时,函数
时,函数![]() 的增区间为
的增区间为![]() ,无减区间;
,无减区间;
②当![]() 时,函数
时,函数![]() 的增区间为
的增区间为![]() 、
、![]() ,减区间为
,减区间为![]() ;
;
③当![]() 时,函数
时,函数![]() 的增区间为
的增区间为![]() 、
、![]() ,减区间为
,减区间为![]() .
.
(2)由![]() ,
, ![]() ,
, ![]() ,分类讨论可得:
,分类讨论可得:
①当![]() 时,函数
时,函数![]() 在区间
在区间![]() 仅有一个零点为
仅有一个零点为![]() ;
;
②当![]() 时,函数
时,函数![]() 在区间
在区间![]() 没有零点;
没有零点;
③当![]() 时,函数
时,函数![]() 在区间
在区间![]() 有两个零点.
有两个零点.
试题解析:
(1)![]()
![]() ,
,
①当![]() 时,
时, ![]() ,故函数
,故函数![]() 的增区间为
的增区间为![]() ,无减区间;
,无减区间;
②当![]() 时,令
时,令![]() ,得
,得![]() 或
或![]() ,
,
故函数![]() 的增区间为
的增区间为![]() 、
、![]() ,减区间为
,减区间为![]() ;
;
③当![]() 时,令
时,令![]() ,得
,得![]() 或
或![]() ,
,
故函数![]() 的增区间为
的增区间为![]() 、
、![]() ,减区间为
,减区间为![]() .
.
(2)由![]() ,
, ![]() ,
, ![]() ,
,
①当![]() 时,
时, ![]() ,此时函数
,此时函数![]() 在区间
在区间![]() 仅有一个零点为
仅有一个零点为![]() ;
;
②当![]() 时,
时, ![]() ,此时函数
,此时函数![]() 在区间
在区间![]() 没有零点;
没有零点;
③当![]() 时,
时, ![]() ,
, ![]() ,此时函数
,此时函数![]() 在区间
在区间![]() 有两个零点.
有两个零点.


 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案科目:高中数学 来源: 题型:
【题目】某城镇社区为了丰富辖区内广大居民的业余文化生活,创建了社区“文化丹青”大型活动场所,配备了各种文化娱乐活动所需要的设施,让广大居民健康生活、积极向上,社区最近四年内在“文化丹青”上的投资金额统计数据如表: (为了便于计算,把2015年简记为5,其余以此类推)
年份 | 5 | 6 | 7 | 8 |
投资金额 | 15 | 17 | 21 | 27 |
(Ⅰ)利用所给数据,求出投资金额![]() 与年份
与年份![]() 之间的回归直线方程
之间的回归直线方程![]() ;
;
(Ⅱ) 预测该社区在2019年在“文化丹青”上的投资金额.
附:对于一组数据![]() , 其回归直线
, 其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为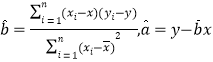 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某连锁经营公司所属5个零售店某月的销售额和利润额资料如表所示:
商店名称 | A | B | C | D | E |
销售额(x)/千万元 | 3 | 5 | 6 | 7 | 9 |
利润额(y)/百万元 | 2 | 3 | 3 | 4 | 5 |
(1)画出销售额和利润额的散点图.
(2)若销售额和利润额具有相关关系,用最小二乘法计算利润额y对销售额x的回归直线方程![]() =
=![]() x+
x+![]() ,其中
,其中![]() =
=![]() ,
,![]() =
=![]() -
-![]()
![]() .
.
(3)若获得利润是4.5百万元时估计销售额是多少(千万元)?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】x的取值范围为[0,10],给出如图所示程序框图,输入一个数x.
(1)请写出程序框图所表示的函数表达式;
(2)求输出的y(y<5)的概率;
(3)求输出的y(6<y≤8)的概率.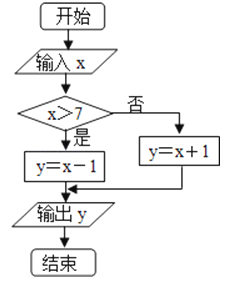
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以坐标原点为极点, ![]() 轴的非负半轴为极轴建立极坐标系,已知曲线
轴的非负半轴为极轴建立极坐标系,已知曲线![]() :
:![]() ,点
,点![]() 的极坐标为
的极坐标为![]() ,直线
,直线![]() 的极坐标方程为
的极坐标方程为![]() ,且点
,且点![]() 在直线
在直线![]() 上.
上.
(1)求曲线![]() 的极坐标方程和直线
的极坐标方程和直线![]() 的直角坐标方程;
的直角坐标方程;
(2)设![]() 向左平移
向左平移![]() 个单位长度后得到
个单位长度后得到![]() ,
,![]() 到
到![]() 的交点为
的交点为![]() ,
, ![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有关部门要了解甲型H1N1流感预防知识在学校的普及情况,命制了一份有10道题的问卷到各个学校做问卷调查。某中学A,B两个班各被随机抽取5名学生接受问卷调查,A班5名学生得分分别为;5, 8, 9, 9, 9:B班5名学生的得分分别为;6, 7, 8, 9, 10。
(1)请你分析A,B两个班中哪个班的问卷得分要稳定些;
(2)如果把B班5名学生的得分看成一个总体,并用简单随机抽样方法从中抽取容量为2的样本,求样本平均数与总体平均数之差的绝对值不小于1的概率。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com