
分析 由正实数a,b,c满足a+b2+c3=1,运用三元均值不等式,可得ab2c3≤$\frac{1}{27}$,再由均值不等式即可得证.
解答 证明:因为正实数a,b,c满足a+b2+c3=1,
所以$1≥3\root{3}{{a{b^2}{c^3}}}$,即$a{b^2}{c^3}≤\frac{1}{27}$,
所以$\frac{1}{{a{b^2}{c^3}}}≥27$,
因此$\frac{1}{a^2}+\frac{1}{b^4}+\frac{1}{c^6}≥3\root{3}{{\frac{1}{{{a^2}{b^4}{c^6}}}}}≥27$.
点评 本题考查不等式的证明,注意运用三元均值不等式,考查化简整理的运算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
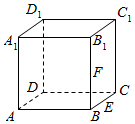
| A. | 直线AA1 | B. | 直线A1B1 | C. | 直线A1D1 | D. | 直线B1C1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 今年暑假期间,雅礼中学组织学生进社区开展社会实践活动.部分学生进行了关于“消防安全”的调查,随机抽取了50名居民进行问卷调查,活动结束后,对问卷结果进行了统计,并将其中“是否知道灭火器使用方法(知道或不知道)”的调查结果统计如表:
今年暑假期间,雅礼中学组织学生进社区开展社会实践活动.部分学生进行了关于“消防安全”的调查,随机抽取了50名居民进行问卷调查,活动结束后,对问卷结果进行了统计,并将其中“是否知道灭火器使用方法(知道或不知道)”的调查结果统计如表:| 年龄(岁) | [10,20) | [20,30) | [30,40) | [40,50) | [50,60) | [60,70] |
| 频数 | m | n | 14 | 12 | 8 | 6 |
| 知道的人数 | 3 | 4 | 8 | 7 | 3 | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com