Question

【题目】在如图所示的几何体中，四边形ABCD是正方形，PA⊥平面ABCD，E，F分别是线段AD，PB的中点，PA＝AB＝1.

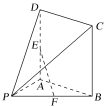
(1)证明：EF∥平面PDC；

(2)求点F到平面PDC的距离.

Answer 1

【答案】（1）证明见解析（2）

【解析】

（1）把向上平移，与重合，则应在上，因此得辅助线作法，取中点，连接，只要证明即可证线面平行；

（2）由（1）只要求到平面的距离即可，这可用体积法求解，即．

(1)证明取PC的中点M，连接DM，MF，

∵M，F分别是PC，PB的中点，∴MF∥CB，MF＝CB，

∵E为DA的中点，四边形ABCD为正方形，

∴DE∥CB，DE＝CB，

∴MF∥DE，MF＝DE，∴四边形DEFM为平行四边形，

∴EF∥DM，∵EF平面PDC，DM平面PDC，

∴EF∥平面PDC.

(2)解∵EF∥平面PDC，∴点F到平面PDC的距离等于点E到平面PDC的距离.

∵PA⊥平面ABCD，∴PA⊥DA，在Rt△PAD中，PA＝AD＝1，∴DP＝.

∵PA⊥平面ABCD，∴PA⊥CB，∵CB⊥AB，PA∩AB＝A，∴CB⊥平面PAB，

∴CB⊥PB，则PC＝，∴PD2＋DC2＝PC2，

∴△PDC为直角三角形，

∴S△PDC＝.

连接EP，EC，易知VE－PDC＝VC－PDE，设E到平面PDC的距离为h，

∵CD⊥AD，CD⊥PA，AD∩PA＝A，∴CD⊥平面PAD，

则×h×＝×1×××1，∴h＝，

∴点F到平面PDC的距离为.