
| A. | (7,1) | B. | (-7,-1) | C. | (-7,1) | D. | (7,-1) |
分析 根据题意,由数乘向量的运算性质可得3$\overrightarrow{a}$=(-9,3),2$\overrightarrow{b}$=(-2,4),进而由向量的坐标运算公式可得3$\overrightarrow{a}$-2$\overrightarrow{b}$的坐标,即可得答案.
解答 解:根据题意,已知$\overrightarrow{a}$=(-3,1),$\overrightarrow{b}$=(-1,2),
则有3$\overrightarrow{a}$=(-9,3),2$\overrightarrow{b}$=(-2,4),
故3$\overrightarrow{a}$-2$\overrightarrow{b}$=(-7,-1);
故选:B.
点评 本题考查平面向量的坐标运算,解题的关键是掌握平面向量坐标运算的性质.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 4i | C. | $\frac{4}{5}$i | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①③ | B. | ②④ | C. | ③④ | D. | ①② |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 3 | C. | ±3 | D. | -3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
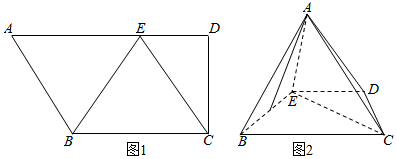
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com