
分析 可作出图形,设圆心为C,从而$|\overrightarrow{OC}|=3$,而由圆的标准方程可得$|\overrightarrow{CA}|=1$,而根据向量的加法和数乘的几何意义可得到$\overrightarrow{OA}=\overrightarrow{OC}+\overrightarrow{CA}$,$\overrightarrow{OB}=\overrightarrow{OC}-\overrightarrow{CA}$,从而进行数量积的运算便可得出$\overrightarrow{OA}•\overrightarrow{OB}$的值.
解答 解:如图,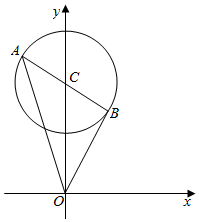
设圆心为C(0,3),则$|\overrightarrow{OC}|=3$;
由圆的标准方程知,圆的半径为1,∴$|\overrightarrow{CA}|=1$;
∴$\overrightarrow{OA}•\overrightarrow{OB}=(\overrightarrow{OC}+\overrightarrow{CA})•(\overrightarrow{OC}+\overrightarrow{CB})$
=$(\overrightarrow{OC}+\overrightarrow{CA})•(\overrightarrow{OC}-\overrightarrow{CA})$
=${\overrightarrow{OC}}^{2}-{\overrightarrow{CA}}^{2}$
=9-1
=8.
故答案为:8.
点评 考查圆的标准方程,以及向量加法和数乘的几何意义,向量数量积的运算,平方差公式在数量积运算中的应用.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:高中数学 来源: 题型:解答题
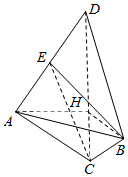 如图,在Rt△ACD中,AH⊥CD,H为垂足,CD=4,AD=2$\sqrt{3}$,∠CAD=90°,以CD为轴,将△ACD按逆时针方向旋转90°到△BCD位置,E为AD中点;
如图,在Rt△ACD中,AH⊥CD,H为垂足,CD=4,AD=2$\sqrt{3}$,∠CAD=90°,以CD为轴,将△ACD按逆时针方向旋转90°到△BCD位置,E为AD中点;查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-2,$\frac{7}{6}$) | B. | ($\frac{7}{6}$,+∞) | C. | [-2,$\frac{7}{6}$) | D. | (-2,-$\frac{7}{6}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (7,1) | B. | (-7,-1) | C. | (-7,1) | D. | (7,-1) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 某校对高二年级进行了一次学业水平模块测试,从该年级学生中随机抽取部分学生,将他们的数学测试成绩分为6组:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100)加以统计,得到如图所示的频率分布直方图.已知高二年级共有学生600名,若成绩不少于80分的为优秀,据此估计,高二年级在这次测试中数学成绩优秀的学生人数为( )
某校对高二年级进行了一次学业水平模块测试,从该年级学生中随机抽取部分学生,将他们的数学测试成绩分为6组:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100)加以统计,得到如图所示的频率分布直方图.已知高二年级共有学生600名,若成绩不少于80分的为优秀,据此估计,高二年级在这次测试中数学成绩优秀的学生人数为( )| A. | 80 | B. | 90 | C. | 120 | D. | 150 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=cos2x | B. | y=2|sinx| | C. | y=($\frac{1}{3}$)cosx | D. | y=tanx |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com