
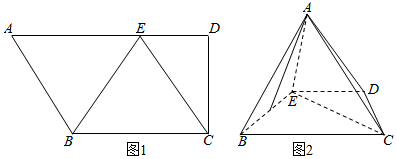
分析 (1)当λ=1时,根据向量数量积的定义求出AFC是等腰直角三角形,结合面面垂直的判定定理即可证明平面ABE⊥平面BCDE;
(2)当λ=2时,得到三棱锥A-BCE是正三棱锥,作出二面角的平面角即可求二面角A-CD-B的余弦值.
解答 证明:(1)在梯形ABCD中,AE=AB=BC=2,∠A=60°,
∴四边形ABCE是菱形,CD=EG=$\sqrt{3}$,DE=1,AF=FC=$\sqrt{3}$,
当λ=1时,则$\overrightarrow{BA}$•$\overrightarrow{BC}$=AB•BCcos∠ABC=2×2cos∠ABC=1,
即cos∠ABC=$\frac{1}{4}$.
则在四棱锥中AC=$\sqrt{A{B}^{2}+B{C}^{2}-2AB•BCcos∠ABC}$=$\sqrt{4+4-2×2×2×\frac{1}{4}}$=$\sqrt{8-2}$=$\sqrt{6}$,
则满足AF2+FC2=AC2,即△AFC是等腰直角三角形,
则AF⊥FC,
∵AF⊥BE,BE∩FC=F,
∴AF⊥平面BCDE,
∵AF?平面ABE,
∴平面ABE⊥平面BCDE.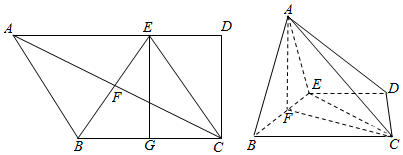
(2)若当λ=2时,$\overrightarrow{BA}$•$\overrightarrow{BC}$=AB•BCcos∠ABC=2×2cos∠ABC=2,
即cos∠ABC=$\frac{1}{2}$.
则△ABC,△AEC是正三角形,
即三棱锥A-BCE是正三棱锥,则A在底面的射影是底面△BCE的中心O,
在梯形ABCD中,过B作BH⊥EC,则H是EC的中点,连接AC交BH于O,
则O是△BCE的中心,
过O作OK⊥CD,
则OK=DE=1,CK=OKtan30°=$\frac{\sqrt{3}}{3}$,
连接AK,则AK⊥CD,
即∠AKO是二面角A-CD-B的平面角,
则AK=$\sqrt{A{C}^{2}-C{K}^{2}}$=$\sqrt{4-(\frac{\sqrt{3}}{3})^{2}}$=$\frac{\sqrt{33}}{3}$,
则cos∠AKO=$\frac{OK}{AK}$=$\frac{1}{\frac{\sqrt{33}}{3}}$=$\frac{\sqrt{33}}{11}$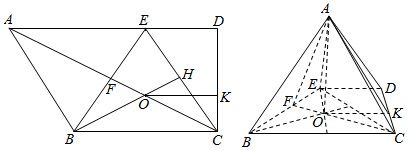
即二面角A-CD-B的余弦值是$\frac{\sqrt{33}}{11}$.
点评 本题主要考查面面垂直的判断以及二面角的求解,根据向量数量积的定义分别确定AC的长度是解决本题的关键.综合性较强,难度较大.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{x^2}{5}-\frac{y^2}{4}=1$ | B. | $\frac{x^2}{4}-\frac{y^2}{5}=1$ | C. | $\frac{x^2}{3}-\frac{y^2}{6}=1$ | D. | $\frac{x^2}{6}-\frac{y^2}{3}=1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (7,1) | B. | (-7,-1) | C. | (-7,1) | D. | (7,-1) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 某校对高二年级进行了一次学业水平模块测试,从该年级学生中随机抽取部分学生,将他们的数学测试成绩分为6组:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100)加以统计,得到如图所示的频率分布直方图.已知高二年级共有学生600名,若成绩不少于80分的为优秀,据此估计,高二年级在这次测试中数学成绩优秀的学生人数为( )
某校对高二年级进行了一次学业水平模块测试,从该年级学生中随机抽取部分学生,将他们的数学测试成绩分为6组:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100)加以统计,得到如图所示的频率分布直方图.已知高二年级共有学生600名,若成绩不少于80分的为优秀,据此估计,高二年级在这次测试中数学成绩优秀的学生人数为( )| A. | 80 | B. | 90 | C. | 120 | D. | 150 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 《城市规划管理意见》中提出“新建住宅原则上不再建设封闭住宅小区,已建成的住宅小区和单位大院逐步打开”,此消息在网上一石激起千层浪.各种说法不一而足,为了了解居民对“开放小区”认同与否,从[25,55]岁人群中随机抽取了n人进行问卷调查,得如下数据:
《城市规划管理意见》中提出“新建住宅原则上不再建设封闭住宅小区,已建成的住宅小区和单位大院逐步打开”,此消息在网上一石激起千层浪.各种说法不一而足,为了了解居民对“开放小区”认同与否,从[25,55]岁人群中随机抽取了n人进行问卷调查,得如下数据:| 组数 | 分组 | 认同人数 | 认同人数占 本组人数比 |
| 第一组 | [25,30) | 120 | 0.6 |
| 第二组 | [30,35) | 195 | p |
| 第三组 | [35,40) | 100 | 0.5 |
| 第四组 | [40,45) | a | 0.4 |
| 第五组 | [45,50) | 30 | 0.3 |
| 第六组 | [50,55) | 15 | 0.3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
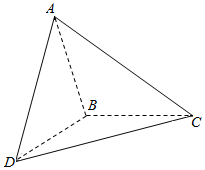 三棱锥A-BCD中,平面ABC⊥平面BCD,AB=BC=BD,∠ABC=∠DBC=120°,则二面角A-BD-C的平面角的正切值是-2.
三棱锥A-BCD中,平面ABC⊥平面BCD,AB=BC=BD,∠ABC=∠DBC=120°,则二面角A-BD-C的平面角的正切值是-2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com