
 �����й滮�����������������½�סլԭ���ϲ��ٽ�����סլС�����ѽ��ɵ�סլС���͵�λ��Ժ��������Ϣ������һʯ����ǧ���ˣ�����˵����һ���㣬Ϊ���˽����ԡ�����С������ͬ���[25��55]����Ⱥ�������ȡ��n�˽����ʾ����飬���������ݣ�
�����й滮�����������������½�סլԭ���ϲ��ٽ�����סլС�����ѽ��ɵ�סլС���͵�λ��Ժ��������Ϣ������һʯ����ǧ���ˣ�����˵����һ���㣬Ϊ���˽����ԡ�����С������ͬ���[25��55]����Ⱥ�������ȡ��n�˽����ʾ����飬���������ݣ�| ���� | ���� | ��ͬ���� | ��ͬ����ռ ���������� |
| ��һ�� | [25��30�� | 120 | 0.6 |
| �ڶ��� | [30��35�� | 195 | p |
| ������ | [35��40�� | 100 | 0.5 |
| ������ | [40��45�� | a | 0.4 |
| ������ | [45��50�� | 30 | 0.3 |
| ������ | [50��55�� | 15 | 0.3 |
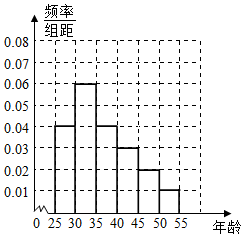
���� ��1����Ƶ��=$\frac{Ƶ��}{����}$��������֪�������������Ƶ�ʷֲ�ֱ��ͼ���������n��a��p��
��2����[40��45�����������ͬ����Ϊ60�ˣ�[45��50����������ͬ����Ϊ30�ˣ����ֲ�����ķ�����9�˲�����̸�ᣬ[40��45��������г�ȡ6�ˣ�[45��50��������г�ȡ3�ˣ��εĿ���ȡֵΪ0��1��2���ֱ������Ӧ�ĸ��ʣ��ɴ�������εķֲ��к���ѧ������
���  �⣺��1����[25��30�����������Ϊx�ˣ�
�⣺��1����[25��30�����������Ϊx�ˣ�
������$\frac{120}{x}=0.6$�����x=200��
��[25��30�������������Ƶ��Ϊ0.04��5=0.2��
��$\frac{200}{n}=0.2$�����n=1000��
��[30��35�������������Ƶ��Ϊ��1-��0.04+0.04+0.03+0.02+0.01����5=0.3��
��[30��35�����������Ϊ0.3��1000=300��
��p=$\frac{195}{300}$=0.65��
��[40��45�������������Ƶ��Ϊ0.03��5=0.15��
��[40��45�����������Ϊ0.15��1000=150��
��a=150��0.4=60��
���Ƶ�ʷֲ�ֱ��ͼ��ͼ��
��2���ɣ�1����[40��45�����������ͬ����Ϊ60�ˣ�[45��50����������ͬ����Ϊ30�ˣ�
���ֲ�����ķ�����9�˲�����̸�ᣬ[40��45��������г�ȡ6�ˣ�[45��50��������г�ȡ3�ˣ�
�εĿ���ȡֵΪ0��1��2��
P����=0��=$\frac{{C}_{3}^{2}}{{C}_{9}^{2}}$=$\frac{1}{12}$��P����=1��=$\frac{{C}_{3}^{1}{C}_{6}^{1}}{{C}_{9}^{2}}$=$\frac{1}{2}$��
P����=2��=$\frac{{C}_{6}^{2}}{{C}_{9}^{2}}$=$\frac{5}{12}$��
�εķֲ���Ϊ��
| �� | 0 | 1 | 2 | |
| P | $\frac{1}{12}$ | $\frac{1}{2}$ | $\frac{5}{12}$ |
���� ���⿼��Ƶ�ʷֲ�ֱ��ͼ��Ƶ�ʷֲ��е�Ӧ�ã�������ɢ����������ķֲ��к���ѧ�����������е��⣬����ʱҪ�������⣬ע���������֪ʶ�ĺ������ã�


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
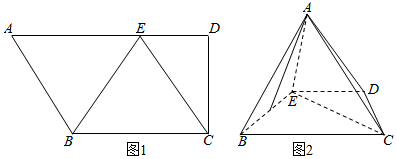
 ��ͼ���ڳ�����ABCD-A1B1C1D1�У�����ABCD�DZ߳�Ϊ2�������Σ���BB1��Ϊ$\sqrt{2}$��������B1-AC-B�Ĵ�С��45�ȣ�
��ͼ���ڳ�����ABCD-A1B1C1D1�У�����ABCD�DZ߳�Ϊ2�������Σ���BB1��Ϊ$\sqrt{2}$��������B1-AC-B�Ĵ�С��45�ȣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | 3 | C�� | ��3 | D�� | -3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��-�ޣ�1�� | B�� | ��-�ޣ�1] | C�� | ��1��+�ޣ� | D�� | [1��+�ޣ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | {2} | B�� | {3} | C�� | {2��3} | D�� | {2��3��4} |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com