Question

4．如图，在长方体ABCD-A₁B₁C₁D₁中，底面ABCD是边长为2的正方形，棱BB₁长为$\sqrt{2}$，则二面角B₁-AC-B的大小是45度．

Answer 1

分析 根据二面角平面角的定义作出二面角的平面角，结合三角形的边角关系进行求解即可．

解答 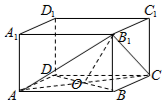解：连接BD交AC于O，连接B₁O，
∵底面ABCD是边长为2的正方形，
∴BO⊥AC，
∵在长方体ABCD-A₁B₁C₁D₁中，B₁B⊥平面ABCD
∴AC⊥平面BBB₁O，AC⊥B₁O，
∴∠B₁OB是二面角B₁-AC-B的平面角，
∵底面ABCD是边长为2的正方形，棱BB₁长为$\sqrt{2}$，
∴OB=$\sqrt{2}$，
则tan∠B₁OB=$\frac{B{B}_{1}}{BO}=\frac{\sqrt{2}}{\sqrt{2}}=1$，
则∠B₁OB=45°，
即二面角B₁-AC-B的大小是45°，
故答案为：45°．

点评 本题主要考查二面角的求解，根据二面角平面角的定义作出二面角的平面角是解决本题的关键．比较基础．