练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    20．若函数f（x）=1-2x，g[f（x）]=$\frac{1-{x}^{2}}{{x}^{2}}$（x≠0），则g（3）=（　　）
    A．1B．0C．15D．30

    分析 由f（x）=1-2x=3，得x=-1，从而g（3）=g[f（-1）]，由此能求出结果．

    解答 解：∵函数f（x）=1-2x，g[f（x）]=$\frac{1-{x}^{2}}{{x}^{2}}$（x≠0），
    ∴由f（x）=1-2x=3，得x=-1，
    ∴g（3）=g[f（-1）]=$\frac{1-（-1）^{2}}{（-1）^{2}}$=0．
    故选：B．

    点评 本题考查函数值的求法，是基础题，解题时要认真审题，注意函数性质的合理运用．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    10．对等式sin（α+β）=sinα+sinβ的认识正确的是（　　）
    A．对于任意的角α、β都成立B．只对α、β取几个特殊值时成立
    C．对于任意的角α、β都不成立D．有无限个α、β的值使等式成立

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    11．已知直线l的参数方程为$\left\{\begin{array}{l}{x=m+\frac{\sqrt{2}}{2}t}\\{y=\frac{\sqrt{2}}{2}t}\end{array}\right.$（t为参数），以坐标原点为极点，x轴的正半轴为极轴建立极坐标系，曲线C的极坐标方程为ρ2（1+2sin2θ）=12，且曲线C的左焦点F在直线l上．
    （I）求实数m和曲线C的直角坐标方程；
    （Ⅱ）若直线l与曲线C交于A，B两点，求$\frac{1}{|AF|}$+$\frac{1}{|BF|}$的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    8．已知函数f（x）=$\frac{1}{2}$x2-2ax-aln（2x）在（1，2）上单调递减，则a的取值范围是[$\frac{4}{5}$，+∞）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    15．过点（2，4）作函数y=x3-2x的切线，则切线方程是y=10x-16或y=x+2．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

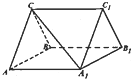    5．如图，三棱柱ABC-A1B1C1中，CA=CB，AB=AA1，∠BAA1=60°．
    （1）证明：AB⊥A1C；
    （2）若AB=CB=2，A1C=$\sqrt{6}$，
    （理科做）求二面角B-AC-A1的余弦值．
    （文科做）求三棱锥A-CA1B的体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

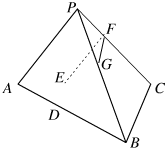    12．如图，平面α截三棱锥P-ABC得截面DEFG，设PA∥α，BC∥α．
    （1）求证：四边形DEFG为平行四边形；
    （2）设PA=6，BC=4，PA与BC所成的角为600，求四边形DEFG面积的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    2．某初级中学有学生270人，其中一年级108人，二、三年级各81人，现要利用抽样方法抽取10人参加某项调查，考虑选用简单随机抽样、分层抽样和系统抽样三种方案，使用简单随机抽样和分层抽样时，将学生按一、二、三年级依次统一编号为1，2，…，270；使用系统抽样时，将学生统一随机编号为1，2，…，270，并将整个编号依次分为10段．如果抽得号码有下列四种情况：
    ①7，34，61，88，115，142，169，196，223，250；
    ②5，9，100，107，111，121，180，195，200，265；
    ③11，38，65，92，119，146，173，200，227，254；
    ④27，54，81，128，135，162，189，216，243，270；
    关于上述样本的下列结论中，可能为系统抽样的是①③；可能为分层抽样的是①②③．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    3．在△ABC中，∠A，∠B，∠C的对边分别为a，b，c，若$\overrightarrow{AB}$•$\overrightarrow{AC}$=$\overrightarrow{BA}$•$\overrightarrow{BC}$=1．
    （1）求证：∠A=∠B；
    （2）求边长c的值；
    （3）若|$\overrightarrow{AB}$+$\overrightarrow{AC}$|=6，求△ABC的面积．

    查看答案和解析>>

    同步练习册答案