
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:高中数学 来源:2014-2015学年广东省广州市毕业班综合测试二理科数学试卷(解析版) 题型:填空题
(几何证明选讲选做题)如图,在平行四边形 中,
中,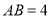 ,点
,点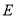 为边
为边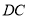 的中点,
的中点,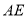 与
与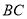 的延长线交于点
的延长线交于点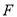 ,且
,且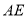 平分
平分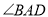 ,作
,作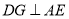 ,垂足为
,垂足为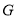 ,若
,若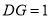 ,则
,则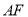 的长为 .
的长为 .

查看答案和解析>>
科目:高中数学 来源:2014-2015学年天津市河西区高三下学期总复习质量调查一文科数学试卷(解析版) 题型:解答题
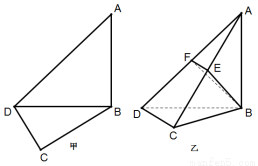
(本小题满分13分)如图甲,在平面四边形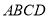 中,已知
中,已知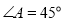 ,
,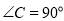 ,
,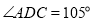 ,
,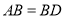 ,现将四边形
,现将四边形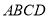 沿
沿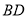 折起,使平面
折起,使平面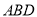
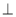 平面
平面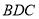 (如图乙),设点
(如图乙),设点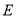 ,
, 分别为棱
分别为棱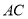 ,
, 的中点.
的中点.
(1)证明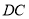
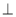 平面
平面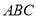 ;
;
(2)求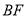 与平面
与平面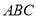 所成角的正弦值;
所成角的正弦值;
(3)求二面角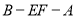 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年天津市河西区高三下学期总复习质量调查一文科数学试卷(解析版) 题型:填空题
某校选修乒乓球课程的学生中,高一年级有40名,高二年级有50名现用分层抽样的方法在这90名学生中抽取一个样本,已知在高一年级的学生中抽取了8名,则在高二年级的学生中应抽取的人数为 .
查看答案和解析>>
科目:高中数学 来源:2014-2015学年天津市河西区高三下学期总复习质量调查一理科数学试卷(解析版) 题型:解答题
(本小题满分14分)已知等差数列 的公差为
的公差为 ,前
,前 项和为
项和为 ,且
,且 ,
, ,
, 成等比数列.
成等比数列.
(1)求数列 的通项公式;
的通项公式;
(2)令
 ,求数列
,求数列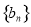 的前
的前 项和
项和 .
.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年天津市河西区高三下学期总复习质量调查一理科数学试卷(解析版) 题型:填空题
以平面直角坐标系的原点为极点, 轴的正半轴为极轴,建立极坐标系,两种
轴的正半轴为极轴,建立极坐标系,两种
坐标系中取相同的长度单位.已知直线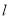 的参数方程是
的参数方程是 (
(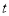 为参数),圆
为参数),圆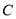 的极坐标方程是
的极坐标方程是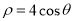 ,则直线
,则直线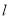 被圆
被圆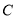 截得的弦长为 .
截得的弦长为 .
查看答案和解析>>
科目:高中数学 来源:2014-2015学年上海市长宁区、嘉定区高三二模文科数学试卷(解析版) 题型:选择题
设双曲线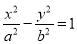 (
(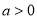 ,
,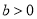 )的虚轴长为
)的虚轴长为 ,焦距为
,焦距为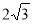 ,则双曲线的渐近线方程为( )
,则双曲线的渐近线方程为( )
A.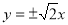 B.
B.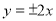 C.
C.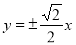 D.
D.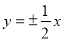
查看答案和解析>>
科目:高中数学 来源:2014-2015学年上海市闵行区高三下学期质量调研考试(二模)文科数学试卷(解析版) 题型:解答题
(本题满分16分)本题共有3个小题,第(1)小题满分4分,第(2)小题满分6分,第(3)小题满分6分.
已知两动圆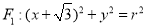 和
和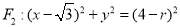 (
(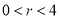 ),把它们的公共点的轨迹记为曲线
),把它们的公共点的轨迹记为曲线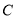 ,若曲线
,若曲线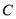 与
与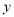 轴的正半轴的交点为
轴的正半轴的交点为 ,且曲线
,且曲线 上的相异两点
上的相异两点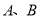 满足:
满足: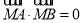 .
.
求曲线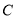 的方程;
的方程;
若 的坐标为
的坐标为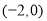 ,求直线
,求直线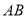 和
和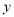 轴的交点
轴的交点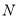 的坐标;
的坐标;
证明直线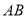 恒经过一定点,并求此定点的坐标.
恒经过一定点,并求此定点的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com