
【题目】已知平面上的线段![]() 及点
及点![]() ,任取
,任取![]() 上的一点
上的一点![]() ,线段
,线段![]() 长度的最小值称为点
长度的最小值称为点![]() 到线段
到线段![]() 的距离,记为
的距离,记为![]() ,设
,设![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,若
,若![]() 满足
满足![]() ,则
,则![]() 关于
关于![]() 的函数解析式为________
的函数解析式为________
【答案】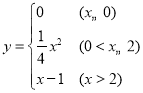
【解析】
寻找平面内到线段![]() 的距离等于到线段
的距离等于到线段![]() 的距离相等的点的轨迹,当
的距离相等的点的轨迹,当![]() 时,
时,![]() 轴上的点到线段
轴上的点到线段![]() 的距离等于到线段
的距离等于到线段![]() 的距离,当
的距离,当![]() 时,点
时,点![]() 到线段
到线段![]() 的距离即为到点
的距离即为到点![]() 的距离,到点
的距离,到点![]() 的距离等于到直线
的距离等于到直线![]() 的距离相等的点的轨迹为抛物线,当
的距离相等的点的轨迹为抛物线,当![]() 时,满足到线段
时,满足到线段![]() 的距离等于到线段
的距离等于到线段![]() 的距离即为到点
的距离即为到点![]() 与到点
与到点![]() 的距离相等点,从而求出
的距离相等点,从而求出![]() 关于
关于![]() 的函数解析式.
的函数解析式.
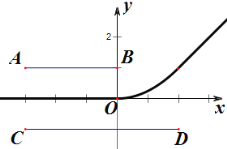
根据题意画出线段![]() 与线段
与线段![]() ,
,
![]() 满足
满足![]() ,
,![]() ,
,![]() ,
,
![]() 点
点![]() 满足到线段
满足到线段![]() 的距离等于到线段
的距离等于到线段![]() 的距离,
的距离,
当![]() 时,
时,![]() 轴上的点到线段
轴上的点到线段![]() 的距离等于到线段
的距离等于到线段![]() 的距离,故
的距离,故![]() ,
,
当![]() 时,点
时,点![]() 到线段
到线段![]() 的距离即为到点
的距离即为到点![]() 的距离,到点
的距离,到点![]() 的距离等于到直线
的距离等于到直线![]() 的距离相等的点的轨迹为抛物线,
的距离相等的点的轨迹为抛物线,
根据抛物线的定义可知点![]() 是抛物线的焦点,
是抛物线的焦点,![]() 是准线,则
是准线,则![]() ,
,
![]() ,即
,即![]() ,
,![]() ,
,
当![]() 时,满足到线段
时,满足到线段![]() 的距离等于到线段
的距离等于到线段![]() 的距离即为到点
的距离即为到点![]() 与到点
与到点![]() 的距离相等点,在平面内到两定点距离相等的点即为线段
的距离相等点,在平面内到两定点距离相等的点即为线段![]() 的垂直平分线,
的垂直平分线,
![]() 点
点![]() 的轨迹为
的轨迹为![]() ,
,
![]() 关于
关于![]() 的函数解析式为:
的函数解析式为: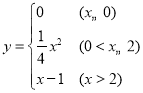 .
.
故答案为: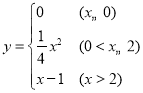 .
.


 步步高达标卷系列答案
步步高达标卷系列答案科目:高中数学 来源: 题型:
【题目】已知直线![]() 与抛物线
与抛物线![]() :
:![]() 交于
交于![]() ,
,![]() 两点,且
两点,且![]() 的面积为16(
的面积为16(![]() 为坐标原点).
为坐标原点).
(1)求![]() 的方程.
的方程.
(2)直线![]() 经过
经过![]() 的焦点
的焦点![]() 且
且![]() 不与
不与![]() 轴垂直,
轴垂直,![]() 与
与![]() 交于
交于![]() ,
,![]() 两点,若线段
两点,若线段![]() 的垂直平分线与
的垂直平分线与![]() 轴交于点
轴交于点![]() ,试问在
,试问在![]() 轴上是否存在点
轴上是否存在点![]() ,使
,使![]() 为定值?若存在,求该定值及
为定值?若存在,求该定值及![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2017年1月至2019年12月期间月接待游客量(单位:万人)的数据,绘制了下面的折线图.根据该折线图,下列结论错误的是( )

A.年接待游客量逐年增加
B.各年的月接待游客量高峰期大致在8月
C.2017年1月至12月月接待游客量的中位数为30万人
D.各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】用一个长为![]() ,宽为
,宽为![]() 的矩形铁皮(如图1)制作成一个直角圆形弯管(如图3):先在矩形的中间画一条曲线,并沿曲线剪开,将所得的两部分分别卷成体积相等的斜截圆柱状(如图2),然后将其中一个适当翻转拼接成直角圆形弯管(如图3)(不计拼接损耗部分),并使得直角圆形弯管的体积最大;
的矩形铁皮(如图1)制作成一个直角圆形弯管(如图3):先在矩形的中间画一条曲线,并沿曲线剪开,将所得的两部分分别卷成体积相等的斜截圆柱状(如图2),然后将其中一个适当翻转拼接成直角圆形弯管(如图3)(不计拼接损耗部分),并使得直角圆形弯管的体积最大;
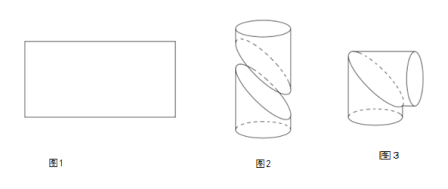
(1)求直角圆形弯管(图3)的体积;
(2)求斜截面椭圆的焦距;
(3)在相应的图1中建立适当的坐标系,使所画的曲线的方程为![]() ,求出方程并画出大致图像;
,求出方程并画出大致图像;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为实数,函数
为实数,函数![]() ,且函数
,且函数![]() 是偶函数,函数
是偶函数,函数![]()
![]() 在区间
在区间![]() 上的减函数,且在区间
上的减函数,且在区间![]() 上是增函数.
上是增函数.
(1)求函数![]() 的解析式;
的解析式;
(2)求实数![]() 的值;
的值;
(3)设![]()
![]() ,问是否存在实数
,问是否存在实数![]() ,使得
,使得![]() 在区间
在区间![]() 上有最小值为
上有最小值为![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下面有五个命题:
①函数![]() 的最小正周期是
的最小正周期是![]() ;
;
②终边在![]() 轴上的角的集合是
轴上的角的集合是![]() ;
;
③在同一坐标系中,函数![]() 的图象和函数
的图象和函数![]() 的图象有三个公共点;
的图象有三个公共点;
④把函数![]() 的图象向右平移
的图象向右平移![]() 个单位得到
个单位得到![]() 的图象;
的图象;
⑤函数![]() 在
在![]() 上是减函数;
上是减函数;
其中真命题的序号是( )
A.①②⑤B.①④C.③⑤D.②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某快递公司在某市的货物转运中心,拟引进智能机器人分拣系统,以提高分拣效率和降低物流成本,已知购买x台机器人的总成本为![]() 万元.
万元.

(1)若使每台机器人的平均成本最低,问应买多少台?
(2)现按(1)中的数量购买机器人,需要安排m人将邮件放在机器人上,机器人将邮件送达指定落袋格口完成分拣(如图).经实验知,每台机器人的日平均分拣量为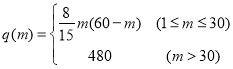 ,(单位:件).已知传统的人工分拣每人每日的平均分拣量为1200件,问引进机器人后,日平均分拣量达最大时,用人数量比引进机器人前的用人数量最多可减少百分之几?
,(单位:件).已知传统的人工分拣每人每日的平均分拣量为1200件,问引进机器人后,日平均分拣量达最大时,用人数量比引进机器人前的用人数量最多可减少百分之几?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,矩形![]() 是一个历史文物展览厅的俯视图,点
是一个历史文物展览厅的俯视图,点![]() 在
在![]() 上,在梯形
上,在梯形![]() 区域内部展示文物,
区域内部展示文物,![]() 是玻璃幕墙,游客只能在
是玻璃幕墙,游客只能在![]() 区域内参观.在
区域内参观.在![]() 上点
上点![]() 处安装一可旋转的监控摄像头.
处安装一可旋转的监控摄像头.![]() 为监控角,其中
为监控角,其中![]() 、
、![]() 在线段
在线段![]() (含端点)上,且点
(含端点)上,且点![]() 在点
在点![]() 的右下方.经测量得知:
的右下方.经测量得知:![]() 米,
米,![]() 米,
米,![]() 米,
米,![]() .记
.记![]() (弧度),监控摄像头的可视区域
(弧度),监控摄像头的可视区域![]() 的面积为
的面积为![]() 平方米.
平方米.

(1)求![]() 关于
关于![]() 的函数关系式,并写出
的函数关系式,并写出![]() 的取值范围;(参考数据:
的取值范围;(参考数据:![]() )
)
(2)求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:极坐标与参数方程
已知在平面直角坐标系xOy中,O为坐标原点,曲线C: 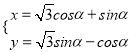 (α为参数),在以平面直角坐标系的原点为极点,x轴的正半轴为极轴,取相同单位长度的极坐标系,直线l:ρ
(α为参数),在以平面直角坐标系的原点为极点,x轴的正半轴为极轴,取相同单位长度的极坐标系,直线l:ρ![]() .
.
(Ⅰ)求曲线C的普通方程和直线l的直角坐标方程;
(Ⅱ)曲线C上恰好存在三个不同的点到直线l的距离相等,分别求出这三个点的极坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com