Question

1．平行四边形ABCD中，AD=1，∠BAD=60°，E为CD中点．若$\overrightarrow{AC}$•$\overrightarrow{BE}$=1，则|AB|=（　　）

• A． 1
• B． $\frac{1}{2}$
• C． $\frac{1}{3}$
• D． $\frac{1}{4}$

Answer 1

分析 利用向量的三角形法则和平行四边形法则和数量积得运算即可得出．

解答 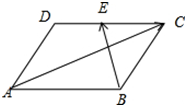解：∵E为CD中点，
∴$\overrightarrow{AC}$•$\overrightarrow{BE}$=（$\overrightarrow{AB}+\overrightarrow{AD}$）•（$\overrightarrow{BC}$-$\overrightarrow{EC}$）
=（$\overrightarrow{AB}+\overrightarrow{AD}$）•（$\overrightarrow{AD}$-$\frac{1}{2}$$\overrightarrow{AB}$）
=$\overrightarrow{AD}$²+$\frac{1}{2}$$\overrightarrow{AB}$•$\overrightarrow{AD}$-$\frac{1}{2}$$\overrightarrow{AB}$²=1+$\frac{1}{2}$|$\overrightarrow{AB}$|cos60°-$\frac{1}{2}$|$\overrightarrow{AB}$|²=1，
即2|$\overrightarrow{AB}$|²-|$\overrightarrow{AB}$|=0，
解得|$\overrightarrow{AB}$|=$\frac{1}{2}$，
即|AB|=$\frac{1}{2}$，
故选：B．

点评 本题主要考查向量数量积的应用，熟练掌握向量的三角形法则和平行四边形法则和数量积得运算是解题的关键．