
【题目】已知函数f(x)=loga(1+x),g(x)=loga(1﹣x)其中(a>0且a≠1),设h(x)=f(x)﹣g(x).
(1)求函数h(x)的定义域,判断h(x)的奇偶性,并说明理由;
(2)若f(3)=2,求使h(x)<0成立的x的集合.
科目:高中数学 来源: 题型:
【题目】已知![]() 分别是双曲线E:
分别是双曲线E: ![]()
![]() 的左、右焦点,P是双曲线上一点,
的左、右焦点,P是双曲线上一点, ![]() 到左顶点的距离等于它到渐近线距离的2倍,(1)求双曲线的渐近线方程;(2)当
到左顶点的距离等于它到渐近线距离的2倍,(1)求双曲线的渐近线方程;(2)当![]() 时,
时, ![]() 的面积为
的面积为![]() ,求此双曲线的方程。
,求此双曲线的方程。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某农场计划种植某种新作物,为此对这种作物的两个品种(分别称为品种甲和品种乙)进行田间试验.选取两大块地,每大块地分成![]() 小块地,在总共
小块地,在总共![]() 小块地中,随机选
小块地中,随机选![]() 小块地种植品种甲,另外
小块地种植品种甲,另外![]() 小块地种植品种乙.
小块地种植品种乙.
(1)假设![]() ,求第一大块地都种植品种甲的概率;
,求第一大块地都种植品种甲的概率;
(2)试验时每大块地分成![]() 小块,即
小块,即![]() ,试验结束后得到品种甲和品种乙在各小块地上的每公顷产量(单位:kg/hm2)如下表:
,试验结束后得到品种甲和品种乙在各小块地上的每公顷产量(单位:kg/hm2)如下表:
甲 |
|
|
|
|
|
|
|
|
乙 |
|
|
|
|
|
|
|
|
分别求品种甲和品种乙的每公顷产量的样本平均数和样本方差;根据试验结果,你认为应该种植哪一品种?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设F1,F2分别是椭圆E: ![]() (a>b>0)的左、右焦点,过点F1的直线交椭圆E于A,B两点,|AF1|=3|BF1|,若cos∠AF2B=
(a>b>0)的左、右焦点,过点F1的直线交椭圆E于A,B两点,|AF1|=3|BF1|,若cos∠AF2B=![]() ,则椭圆E的离心率为( )
,则椭圆E的离心率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工程设备租赁公司为了调查A,B两种挖掘机的出租情况,现随机抽取了这两种挖掘机各100台,分别统计了每台挖掘机在一个星期内的出租天数,统计数据如下表:

(I)根据这个星期的统计数据,将频率视为概率,求该公司一台A型挖掘机,一台B型挖掘机一周内合计出租天数恰好为4天的概率;
(II)如果A,B两种挖掘机每台每天出租获得的利润相同,该公司需要从A,B两种挖掘机中购买一台,请你根据所学的统计知识,给出建议应该购买哪一种类型,并说明你的理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
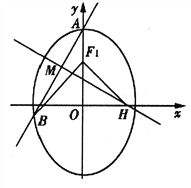
【题目】已知椭圆![]() 的上、下焦点分别为
的上、下焦点分别为![]() ,上焦点
,上焦点![]() 到直线 4x+3y+12=0的距离为3,椭圆C的离心率e=
到直线 4x+3y+12=0的距离为3,椭圆C的离心率e=![]() .
.
(I)求椭圆C的标准方程;
(II)设过椭圆C的上顶点A的直线![]() 与椭圆交于点B(B不在y轴上),垂直于
与椭圆交于点B(B不在y轴上),垂直于![]() 的直线与
的直线与![]() 交于点M,与
交于点M,与![]() 轴交于点H,若
轴交于点H,若![]() =0,且
=0,且![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】孝感市及周边地区的市民游玩又添新去处啦!孝感熙凤水乡旅游度假区于2017年10月1日正式对外开放.据统计,从2017年10月1日到10月7日参观孝感市熙凤水乡旅游度假区的人数如表所示:
日期 | 1日 | 2日 | 3日 | 4日 | 5日 | 6日 | 7日 |
人数(万) | 11 | 13 | 8 | 9 | 7 | 8 | 10 |
(1)把这7天的参观人数看成一个总体,求该总体的众数和平均数(精确到0.1);
(2)用简单随机抽样方法从10月1日到10月4日中抽取2天,它们的参观人数组成一个样本,求该样本平均数与总体平均数之差的绝对值不超过1万的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com