
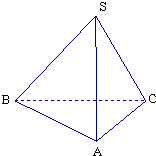
 在三棱锥S-ABC中,∠SAB=∠SAC=∠ACB=90°,AC=1,BC=$\sqrt{3}$,SB=2$\sqrt{2}$.
在三棱锥S-ABC中,∠SAB=∠SAC=∠ACB=90°,AC=1,BC=$\sqrt{3}$,SB=2$\sqrt{2}$.分析 (1)求三棱锥S-ABC的体积,由题设条件得,棱锥的高是SA,底面是直角三角形,体积易求;
(2)证明BC⊥SC,可通过证明BC⊥面ASC来证;
(3)由(1)可知∠BAC为二面角C-SA-B的平面角,利用三角函数,可求二面角C-SA-B的大小.
解答 解:(1)∵∠SAB=∠SAC=∠ACB=90°,
∴SA⊥面BAC,即SA即是棱锥的高,
又AC=1,BC=$\sqrt{3}$,SB=2$\sqrt{2}$,∠ACB=90°,
∴AB=2,SA=2$\sqrt{3}$,
∴三角形BAC的面积为$\frac{1}{2}×1×\sqrt{3}$=$\frac{\sqrt{3}}{2}$,
三棱锥S-ABC的体积为$\frac{1}{3}×\frac{\sqrt{3}}{2}×2\sqrt{3}$=1;
(2)证明:由(1)知SA⊥面BAC可得SA⊥BC,
由∠ACB=90°,可得BC⊥AC,
又SA∩AC=A,
∴BC⊥面SCA,
∴BC⊥SC;
(3)由(1)可知∠BAC为二面角C-SA-B的平面角,
∵AC=1,BC=$\sqrt{3}$,∠ACB=90°
∴tan∠BAC=$\sqrt{3}$,
∴∠BAC=60°,
∴二面角C-SA-B的平面角为60°.
点评 本题考查求三棱锥的体积,线面垂直的判断与性质,考查二面角C-SA-B的平面角,正确运用线面垂直的判定与性质是关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:2017届甘肃会宁县一中高三上学期9月月考数学(文)试卷(解析版) 题型:解答题
已知函数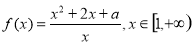 .
.
(1)当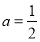 时,求函数
时,求函数 的最小值;
的最小值;
(2)若对任意x∈[1,+∞),f(x)>0恒成立,试求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源:2017届甘肃会宁县一中高三上学期9月月考数学(理)试卷(解析版) 题型:选择题
下列选项中,说法正确的是( )
A.命题“?x0∈R,x-x0≤0”的否定是“?x0∈R,x-x0>0”
B.命题“p∨q为真”是命题“p∧q为真”的充分不必要条件
C.命题“若am2≤bm2,则a≤b”是假命题
D.命题“在△ABC中,若sin A<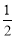 ,则A<
,则A<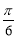 ”的逆否命题为真命题
”的逆否命题为真命题
查看答案和解析>>
科目:高中数学 来源:2017届安徽六安一中高三上学期月考二数学(文)试卷(解析版) 题型:选择题
在平面四边形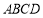 中,满足
中,满足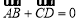 ,
,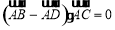 ,则四边形
,则四边形 是( )
是( )
A.菱形 B.正方形 C.矩形 D.梯形
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,正四棱柱ABCD-A1B1C1D1中,AA1=2AB=4,点E在C1C上,且C1E=3EC.
如图,正四棱柱ABCD-A1B1C1D1中,AA1=2AB=4,点E在C1C上,且C1E=3EC.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com