
分析 (1)将极坐标方程转化成直角坐标系方程,求得C点坐标,半径为2,写出圆C的直角坐标方程;
(2)根据矩阵的变换$[\begin{array}{l}{1}&{0}\\{0}&{2}\end{array}]$$[\begin{array}{l}{x}\\{y}\end{array}]$=$[\begin{array}{l}{x′}\\{y′}\end{array}]$,求得$\left\{\begin{array}{l}{x=x′}\\{y=\frac{y′}{2}}\end{array}\right.$,将x′及y′代入圆C方程,即可求得曲线C1的方程;
(3)将参数方程转化为普通方程,l过圆心,弦长就等于直径,即可求得所截得的弦长.
解答 解:(1)在平面直角坐标系中,$\left\{\begin{array}{l}{x=ρcosθ}\\{y=ρsinθ}\end{array}\right.$,
∴$\left\{\begin{array}{l}{x=\sqrt{3}}\\{y=1}\end{array}\right.$,C点坐标为:$C({\sqrt{3},1})$…2分
圆C的直角坐标方程:${(x-\sqrt{3})^2}+{(y-1)^2}=4$…4分
(2)由$[\begin{array}{l}{1}&{0}\\{0}&{2}\end{array}]$$[\begin{array}{l}{x}\\{y}\end{array}]$=$[\begin{array}{l}{x′}\\{y′}\end{array}]$,
∴$\left\{\begin{array}{l}{x=x′}\\{y=\frac{y′}{2}}\end{array}\right.$,
将x′及y′代入圆C方程整理得:$4{x^2}+{y^2}-8\sqrt{3}x-4y=0$…10分
(3)将直线的参数方程转化成普通方程得:
直线l:$x-\sqrt{3}y=0$,过圆心,
所以弦长为4.…14分
点评 本题考查极坐标与直角坐标的转化,直线参数方程转化普通方程,矩阵的变换,考查转化思想,属于基础题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:2017届甘肃会宁县一中高三上学期9月月考数学(文)试卷(解析版) 题型:解答题
选修4—5:不等式选讲
已知函数f(x)=|2x-a|+a.
(1)若不等式f(x)≤6的解集为{x|-2≤x≤3},求实数a的值;
(2)在(1)的条件下,若存在实数n使f(n)≤m-f(-n)成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源:2017届安徽六安一中高三上学期月考二数学(文)试卷(解析版) 题型:选择题
设向量 与
与 满足
满足 ,
, 在
在 方向上的投影为1,若存在实数
方向上的投影为1,若存在实数 ,使得
,使得 与
与 垂直,则
垂直,则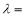 ( )
( )
A.3 B.2 C.1 D.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
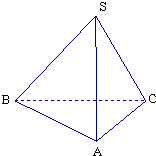 在三棱锥S-ABC中,∠SAB=∠SAC=∠ACB=90°,AC=1,BC=$\sqrt{3}$,SB=2$\sqrt{2}$.
在三棱锥S-ABC中,∠SAB=∠SAC=∠ACB=90°,AC=1,BC=$\sqrt{3}$,SB=2$\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| API | [0,50] | (50,100] | (100,150] | (150,200] | (200,300] | >300 |
| 空气质量 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 重度污染 |
| 天数 | 6 | 14 | 18 | 27 | 20 | 15 |
| 非严重污染 | 严重污染 | 合计 | |
| 供暖季 | 22 | 8 | 30 |
| 非供暖季 | 63 | 7 | 70 |
| 合计 | 85 | 15 | 100 |
| P(K2≥k) | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| k | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
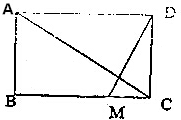 如图所示,一个矩形花园需要铺设两条笔直的小路,已知花园的长AD=5m,宽AB=3m,其中一条小路定为AC,另一条小路过点D,问是否在BC上存在一点M,使得两条小路,AC、DM互相垂直?若存在,求出小路DM的长.
如图所示,一个矩形花园需要铺设两条笔直的小路,已知花园的长AD=5m,宽AB=3m,其中一条小路定为AC,另一条小路过点D,问是否在BC上存在一点M,使得两条小路,AC、DM互相垂直?若存在,求出小路DM的长.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com