练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
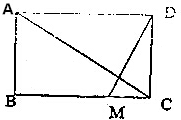
    10．如图所示，一个矩形花园需要铺设两条笔直的小路，已知花园的长AD=5m，宽AB=3m，其中一条小路定为AC，另一条小路过点D，问是否在BC上存在一点M，使得两条小路，AC、DM互相垂直？若存在，求出小路DM的长．

    分析 建立直角坐标系，求出相关点的坐标，求出直线DM的方程，然后求解M的坐标，即可求出小路DM的长．

    解答 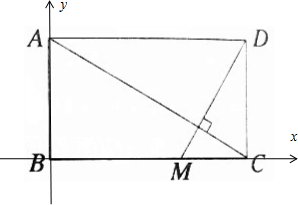解：以B为坐标原点，BC所在直线为x轴，BA所在直线为y轴，
    则：B（0，0），A（0，3），C（5，0），D（5，3），
    kAC=-$\frac{3}{5}$，两条小路所在直线AC与DM相互垂直，可得kDM=$\frac{5}{3}$，DM所在直线方程为：y-3=$\frac{5}{3}$（x-5）．
    令y=0可得：x=$\frac{16}{5}$．
    M所在位置距离B为：$\frac{16}{5}$m．
    ∴CM=$\frac{9}{5}$，∴DM=$\sqrt{9+\frac{81}{25}}$=$\frac{3\sqrt{34}}{5}$m．

    点评 本题考查直线方程的综合应用，直线垂直关系的应用，考查计算能力．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2017届甘肃会宁县一中高三上学期9月月考数学（理）试卷（解析版） 题型：解答题

    已知函数.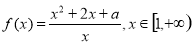

    （1）当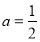时，求函数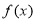的最小值；

    （2）若对任意x∈[1，＋∞），f（x）>0恒成立，试求实数a的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    1．在极坐标系中，圆C是以点$C（{2，\frac{π}{6}}）$为圆心，2为半径的圆．
    （1）求圆C的直角坐标方程；
    （2）圆C在矩阵$A=[\begin{array}{l}1\\ 0\end{array}\right.$$\left.\begin{array}{l}0\\ 2\end{array}]$的作用下变换为曲线C1，求曲线C1的方程；
    （3）求圆C被直线$l：\left\{\begin{array}{l}x=\frac{{\sqrt{3}}}{2}t\\ y=\frac{1}{2}t\end{array}\right.$（t为参数）所截得的弦长．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    18．设函数f（x）=|4x-1|+|x-m|．
    （1）若m=2，解不等式f（x）＞12；
    （2）若f（x）+3|x-m|＞8对一切实数x均成立，求实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    5．已知f（x）=xlnx，g（x）=x3+ax2-x+2．
    （Ⅰ）求函数f（x）的极值；
    （Ⅱ）对一切的x∈（0，+∞）时，2f（x）≤g′（x）+2恒成立，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    15．已知|A-a|＜$\frac{?}{2}$，|B-b|＜$\frac{?}{2}$，求证：
    （1）|（A+B）-（a+b）|＜ε；
    （2）|（A-B）-（a-b）|＜ε．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    2．设数列{an}，a2=$\frac{a}{3}$（a为非零常数），an+1=$\frac{{a}_{n}}{3}$+$\frac{a}{{3}^{n}}$，数列{bn}，bn=3n-1an，Sn是数列{bn}的前n项的和．
    （1）求证：数列{bn}为等差数列；
    （2）是否存在实数a、b，使得对任意正整数t，数列{bn}中满足bn+b≤t的最大项恰是第3t-2项？若存在，分别求出a与b的取值范围；若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    19．已知曲线f（x）=axlnx+bx在（1，f（1））处的切线方程为y=x-1．
    （1）求函数f（x）的解析式；
    （2）对?x≥1，不等式f（x）≤m（x2-1）（m＞0）恒成立，求实数m的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    4．下列命题中，正确的是（　　）
    A．有两边及一边的对角对应相等的两个三角形全等
    B．两边相等的两直角三角形全等
    C．有两个角及第三个角的对边对应相等的两个三角形全等
    D．有两个角及一边相等的两个三角形全等

    查看答案和解析>>

    同步练习册答案