
分析 利用绝对值不等式的性质|x+y|≤|x|+|y|、|x|=|-x|、以及不等式的基本性质,证得要证的结论成立.
解答 证明:(1)∵|A-a|<$\frac{?}{2}$,|B-b|<$\frac{?}{2}$,∴|A-a|+|B-b|<$\frac{?}{2}$+$\frac{ε}{2}$=ε.
∵|A-a|+|B-b|≥|(A-a)+( B-b )|=|(A+B)-(a+b)|,
∴|(A+B)-(a+b)|<ε成立.
(2)∵|A-a|<$\frac{?}{2}$,|B-b|<$\frac{?}{2}$,∴|A-a|<$\frac{?}{2}$,|b-B|<$\frac{?}{2}$.
∵|A-a|+|B-b|<$\frac{?}{2}$+$\frac{?}{2}$=ε,
而|A-a|+|B-b|≥|(A-a )+(b-B)|=|(A-B)-(a-b)|,
∴|(A-B)-(a-b)|<ε 成立.
点评 本题主要考查不等式的基本性质,绝对三角不等式的应用,属于中档题.


 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案科目:高中数学 来源: 题型:解答题
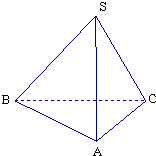 在三棱锥S-ABC中,∠SAB=∠SAC=∠ACB=90°,AC=1,BC=$\sqrt{3}$,SB=2$\sqrt{2}$.
在三棱锥S-ABC中,∠SAB=∠SAC=∠ACB=90°,AC=1,BC=$\sqrt{3}$,SB=2$\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
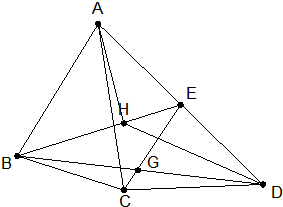 如图,在四边形ABCD中,已知△ABC、△BCD、△ACD的面积之比是3:1:4,点E在边AD上,CE交BD于G,设$\frac{BG}{GD}=\frac{DE}{EA}=k$.
如图,在四边形ABCD中,已知△ABC、△BCD、△ACD的面积之比是3:1:4,点E在边AD上,CE交BD于G,设$\frac{BG}{GD}=\frac{DE}{EA}=k$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
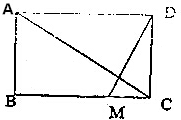 如图所示,一个矩形花园需要铺设两条笔直的小路,已知花园的长AD=5m,宽AB=3m,其中一条小路定为AC,另一条小路过点D,问是否在BC上存在一点M,使得两条小路,AC、DM互相垂直?若存在,求出小路DM的长.
如图所示,一个矩形花园需要铺设两条笔直的小路,已知花园的长AD=5m,宽AB=3m,其中一条小路定为AC,另一条小路过点D,问是否在BC上存在一点M,使得两条小路,AC、DM互相垂直?若存在,求出小路DM的长.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 4$\sqrt{2}$-1 | C. | 2$\sqrt{2}$-2 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com