
分析 (Ⅰ)由已知可得6Sn+1=(an+1+1)(an+1+2),两式相减可得,an+1-an=3,结合等差数列的通项公式可求;
(Ⅱ)由题意可以判断a1=1,an=3n-2,再根据裂项求和,得到$\frac{10}{9}$×(1-$\frac{1}{3n-2}$)≤1,解得即可.
解答 解:(Ⅰ)由题意可得6S1=(a1+1)(a1+2),解得a1=1或a1=2,
由an+1=Sn+1-Sn=$\frac{1}{6}$(an+1+1)(an+1+2)-$\frac{1}{6}$(an+1)(an+2),
可得an+1-an-3=0或an+1+an=0,
∵数列{an}的各项均为正数,
∴an+1=-an不成立,故舍去.
∴an+1-an-3=0.
根据等差数列的定义可得:{an}是公差为3,首项为2的等差数列
或{an}是公差为3,首项为1的等差数列,
∴{an}的通项为an=3n-1,或an=3n-2,
(Ⅱ)由$\frac{10}{3}$($\frac{1}{{a}_{1}{a}_{2}}$$+\frac{1}{{a}_{2}{a}_{3}}$+$\frac{1}{{a}_{3}{a}_{4}}$+…+$\frac{1}{{a}_{n-1}{a}_{n}}$)≤a1<2,
∴a1=1,an=3n-2,
∵$\frac{1}{{a}_{n-1}{a}_{n}}$=$\frac{1}{(3n-5)(3n-2)}$=$\frac{1}{3}$($\frac{1}{3n-5}$-$\frac{1}{3n-2}$),
∴$\frac{10}{3}$($\frac{1}{{a}_{1}{a}_{2}}$$+\frac{1}{{a}_{2}{a}_{3}}$+$\frac{1}{{a}_{3}{a}_{4}}$+…+$\frac{1}{{a}_{n-1}{a}_{n}}$)=$\frac{10}{9}$(1-$\frac{1}{4}$+$\frac{1}{4}$-$\frac{1}{10}$+…+$\frac{1}{3n-5}$-$\frac{1}{3n-2}$)
=$\frac{10}{9}$×(1-$\frac{1}{3n-2}$)≤1,
∴$\frac{1}{3n-2}$≥$\frac{1}{10}$,
即3n-2≤10,
解得n≤4,
故n的最大值为4.
点评 本题考查了数列的递推公式和数列的通项公式的求法,以及裂项求和,以及不等式的解法,属于中档题.


 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案科目:高中数学 来源:2017届甘肃会宁县一中高三上学期9月月考数学(理)试卷(解析版) 题型:选择题
已知定义在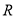 上的奇函数
上的奇函数 满足
满足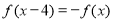 ,且在区间[0,2]上是增函数,则( )
,且在区间[0,2]上是增函数,则( )
A.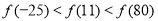 B.
B.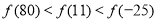
C.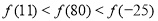 D.
D.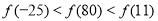
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,正四棱柱ABCD-A1B1C1D1中,AA1=2AB=4,点E在C1C上,且C1E=3EC.
如图,正四棱柱ABCD-A1B1C1D1中,AA1=2AB=4,点E在C1C上,且C1E=3EC.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com