
分析 (1)求出函数的导数,得到k=x2-2x+1≥0,从而求出k的最小值即可;
(2)设$g(x)=e-\frac{e^x}{x}$,得到函数的单调区间,得到g(x)≤g(1)=0,可得a≤0即可.
解答 解:(1)f'(x)=x2-(a+2)x+1
设P(x,y),由于a=0,
所以k=x2-2x+1≥0,
即kmin=0;
(2)设$g(x)=e-\frac{e^x}{x}$,
则$g'(x)=\frac{{{e^x}({1-x})}}{x^2}$,
易知g(x)在(0,1)单调递增,(1,+∞)单调递减,
所以g(x)≤g(1)=0,
由条件知f'(1)≥g(1),可得a≤0
当a≤0时,f'(x)=x2-(a+2)x+1=(x-1)2-ax≥(x-1)2≥0,
∴f'(x)≥g(x)对?x>0成立,
综上,a≤0.
点评 本题考查了切线的斜率问题,考查函数的单调性,导数的应用,是一道中档题.


科目:高中数学 来源:2017届甘肃会宁县一中高三上学期9月月考数学(理)试卷(解析版) 题型:解答题
已知函数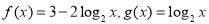 .
.
(1)当x∈[1,4]时,求函数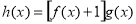 的值域;
的值域;
(2)如果对任意的x∈[1,4],不等式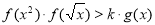 恒成立,求实数k的取值范围
恒成立,求实数k的取值范围
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图1,△ACB为等腰直角三角形,AC=BC,AC⊥BC,点E、F分别在BC上,且CE=BF,CM⊥AE,AE与MF的延长线相交于N点
如图1,△ACB为等腰直角三角形,AC=BC,AC⊥BC,点E、F分别在BC上,且CE=BF,CM⊥AE,AE与MF的延长线相交于N点查看答案和解析>>
科目:高中数学 来源: 题型:解答题
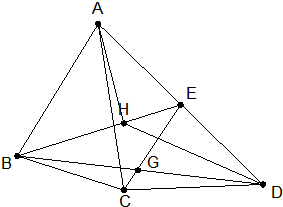 如图,在四边形ABCD中,已知△ABC、△BCD、△ACD的面积之比是3:1:4,点E在边AD上,CE交BD于G,设$\frac{BG}{GD}=\frac{DE}{EA}=k$.
如图,在四边形ABCD中,已知△ABC、△BCD、△ACD的面积之比是3:1:4,点E在边AD上,CE交BD于G,设$\frac{BG}{GD}=\frac{DE}{EA}=k$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com