
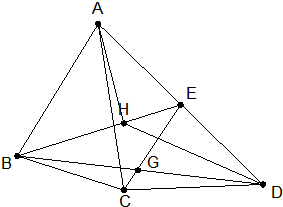
 如图,在四边形ABCD中,已知△ABC、△BCD、△ACD的面积之比是3:1:4,点E在边AD上,CE交BD于G,设$\frac{BG}{GD}=\frac{DE}{EA}=k$.
如图,在四边形ABCD中,已知△ABC、△BCD、△ACD的面积之比是3:1:4,点E在边AD上,CE交BD于G,设$\frac{BG}{GD}=\frac{DE}{EA}=k$.分析 (1)不妨设△ABC、△BCD、△ACD的面积分别为3、1、4,由已知比例关系可得△ABD、△BDE、△CDG、△CDE、△DEG的面积.由此可得:$\frac{1}{k+1}$+$\frac{6k}{{{{(k+1)}^2}}}$=$\frac{4k}{k+1}$,由此可得k值,则$\root{3}{{7{k^2}+20}}$可求;
(2)由(1)知:E、G分别为AD、BD的中点,又∵点H分线段BE成$\frac{BH}{HE}=2$的两段,可得点H是△ABD的重心.延长BE到K,使得BE=EK,连结AK、DK后便得到平行四边形ABDK,再利用“平行四边形的四边平方和等于两对角线的平方和”可得:2(AB2+BD2)=AD2+4BE2,同理有$\left\{{\begin{array}{l}{2(B{D^2}+A{D^2})=A{B^2}+4D{M^2}}\\{2(A{B^2}+A{D^2})=B{D^2}+4A{G^2}}\end{array}}\right.$,得到3(AB2+BD2+AD2)=4(BE2+DM2+AG2).进一步得到AB2+BD2+AD2=3p2.
解答 解:(1)不妨设△ABC、△BCD、△ACD的面积分别为3、1、4,
∵$\frac{BG}{GD}=\frac{DE}{EA}=k$,∴△ABD的面积是6,△BDE的面积是$\frac{6k}{k+1}$,△CDG的面积是$\frac{1}{k+1}$,△CDE的面积为$\frac{4k}{k+1}$,△DEG的面积是$\frac{6k}{{{{(k+1)}^2}}}$.
由此可得:$\frac{1}{k+1}$+$\frac{6k}{{{{(k+1)}^2}}}$=$\frac{4k}{k+1}$,即 4k2-3k-1=0,∴k=1,
∴$\root{3}{{7{k^2}+20}}$=3;
(2)由(1)知:E、G分别为AD、BD的中点,又∵点H分线段BE成$\frac{BH}{HE}=2$的两段,
∴点H是△ABD的重心.
而当延长BE到K,使得BE=EK,连结AK、DK后便得到平行四边形ABDK,
再利用“平行四边形的四边平方和等于两对角线的平方和”可得:2(AB2+BD2)=AD2+4BE2,
同理有$\left\{{\begin{array}{l}{2(B{D^2}+A{D^2})=A{B^2}+4D{M^2}}\\{2(A{B^2}+A{D^2})=B{D^2}+4A{G^2}}\end{array}}\right.$,其中点M为边AB的中点.
∴3(AB2+BD2+AD2)=4(BE2+DM2+AG2).
∵$AH=\frac{2}{3}AG,BH=\frac{2}{3}BE,DH=\frac{2}{3}DM$,AH2+BH2+DH2=p2,
∴$B{E^2}+D{M^2}+A{G^2}=\frac{9}{4}{p^2}$,
∴AB2+BD2+AD2=3p2.
点评 本题考查平行线分线段成比例定理,考查推理论证能力与逻辑运算能力,难度较大.


科目:高中数学 来源:2017届甘肃会宁县一中高三上学期9月月考数学(文)试卷(解析版) 题型:选择题
设集合M={x|-1≤x<2},N={y|y<a},若M∩N≠∅,则实数a的取值范围一定是( )
A.[-1,2) B.(-∞,2] C.[2,+∞) D.(-1,+∞)
查看答案和解析>>
科目:高中数学 来源:2017届安徽六安一中高三上学期月考二数学(文)试卷(解析版) 题型:选择题
在平面四边形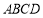 中,满足
中,满足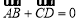 ,
,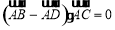 ,则四边形
,则四边形 是( )
是( )
A.菱形 B.正方形 C.矩形 D.梯形
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,正四棱柱ABCD-A1B1C1D1中,AA1=2AB=4,点E在C1C上,且C1E=3EC.
如图,正四棱柱ABCD-A1B1C1D1中,AA1=2AB=4,点E在C1C上,且C1E=3EC.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com