
| A. | 直线过圆心 | B. | 相交但不过圆心 | C. | 相切 | D. | 相离 |
科目:高中数学 来源:2017届安徽六安一中高三上学期月考二数学(文)试卷(解析版) 题型:解答题
已知向量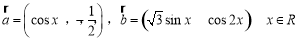 ,设函数
,设函数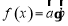 .
.
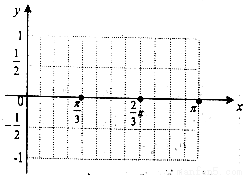
(1)求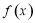 的表达式并完成下面的表格和画出
的表达式并完成下面的表格和画出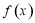 在
在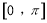 范围内的大致图象;
范围内的大致图象;
0 |
|
|
| |||
| 0 |
| ||||
|
(2)若方程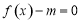 在
在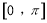 上有两个根
上有两个根 、
、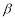 ,求
,求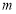 的取值范围及
的取值范围及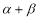 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
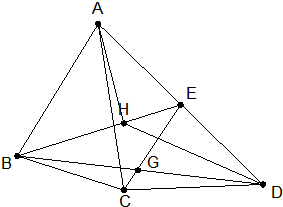 如图,在四边形ABCD中,已知△ABC、△BCD、△ACD的面积之比是3:1:4,点E在边AD上,CE交BD于G,设$\frac{BG}{GD}=\frac{DE}{EA}=k$.
如图,在四边形ABCD中,已知△ABC、△BCD、△ACD的面积之比是3:1:4,点E在边AD上,CE交BD于G,设$\frac{BG}{GD}=\frac{DE}{EA}=k$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 4$\sqrt{2}$-1 | C. | 2$\sqrt{2}$-2 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com