
分析 先根据方程求出x的范围,再利用换元法求得原方程的解.
解答 解:由方程$\sqrt{3x-5}$-$\sqrt{x+2}$=1,可得$\left\{\begin{array}{l}{x+2≥0}\\{3x-5≥0}\end{array}\right.$,∴-2≤x≤$\frac{5}{3}$.
令$\sqrt{x+2}$=t,则t≥0,$\sqrt{{3t}^{2}-11}$-t=1,即$\sqrt{{3t}^{2}-11}$=t+1,
平方可得3t2-11=t2+2t+1,即 t2-t-6=0,求得t=-2 (舍去),或t=3,
即$\sqrt{x+2}$=3,求得x=7,
故原方程的解为x=7.
点评 本题主要考查根式方程的解法,函数零点与方程的跟的关系,属于中档题.


 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:高中数学 来源:2017届安徽六安一中高三上学期月考二数学(文)试卷(解析版) 题型:选择题
在平面四边形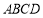 中,满足
中,满足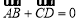 ,
,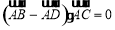 ,则四边形
,则四边形 是( )
是( )
A.菱形 B.正方形 C.矩形 D.梯形
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com