
分析 (Ⅰ)求出函数的导数,二次求导,得到函数的单调区间即可;
(Ⅱ)求出f(x)的导数,构造函数h(x)=2+sinx-(x-a)cosx,通过讨论a的范围,确定函数的单调性,从而求出函数的最大值即可.
解答 解:(Ⅰ)若a=π,则$f(x)=\frac{x-π}{sinx+2}(x∈[0,\frac{π}{2}])$,
$f'(x)=\frac{2+sinx-(x-π)cosx}{{{{(sinx+2)}^2}}}$,
令g(x)=2+sinx-(x-π)cosx,g'(x)=(x-π)sinx<0,
所以g(x)在区间$[0,\frac{π}{2}]$单调递减,且有$g(\frac{π}{2})=3>0$,
所以f'(x)>0,函数f(x)在区间$[0,\frac{π}{2}]$上单调递增;
(Ⅱ)$f'(x)=\frac{2+sinx-(x-a)cosx}{{{{(sinx+2)}^2}}}$,
令h(x)=2+sinx-(x-a)cosx,h'(x)=(x-a)sinx,
1)当$a∈(0,\frac{π}{2})$,x=a是函数g(x)的极小值点,也是最小值点,
∵g(a)=2+sina>0,
∴函数f(x)在区间$[0,\frac{π}{2}]$上单调递增,${f_{max}}=f(\frac{π}{2})=\frac{{\frac{π}{2}-a}}{3}$;
2)当$a∈[\frac{π}{2},+∞)$,h'(x)<0,
函数h(x)在区间$[0,\frac{π}{2}]$上递减,$h(\frac{π}{2})=3>0$,
所以函数f(x)在区间$[0,\frac{π}{2}]$上单调递增,
当$x=\frac{π}{2}$时,函数f(x)取得最大值$f({\frac{π}{2}})=\frac{π}{6}-\frac{a}{3}$;
3)当a∈[-2,0]时h'(x)>0,h(0)=2+a,h(0)≥0,
所以函数f(x)在区间$[0,\frac{π}{2}]$上递增,
当$x=\frac{π}{2}$时,函数f(x)取得最大值$f({\frac{π}{2}})=\frac{π}{6}-\frac{a}{3}$;
综上所述,当a≥-2时,函数f(x)的最大值为$f({\frac{π}{2}})=\frac{π}{6}-\frac{a}{3}$.
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及分类讨论思想,是一道中档题.


 名校通行证有效作业系列答案
名校通行证有效作业系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
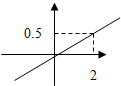 某商场欲经销某种商品,考虑到不同顾客的喜好,决定同时销售A,B两个品牌,根据生产厂家营销策略,结合本地区以往经销该商品的数据统计分析,A品牌的销售利润y1与投入资金x成正比,其关系如图所示,B品牌的销售利润y2与投入资金x的关系为y2=$\frac{3}{4}\sqrt{x}$.
某商场欲经销某种商品,考虑到不同顾客的喜好,决定同时销售A,B两个品牌,根据生产厂家营销策略,结合本地区以往经销该商品的数据统计分析,A品牌的销售利润y1与投入资金x成正比,其关系如图所示,B品牌的销售利润y2与投入资金x的关系为y2=$\frac{3}{4}\sqrt{x}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 近几年骑车锻炼越来越受到人们的喜爱,男女老少踊跃参加,我校课外活动小组利用春节放假时间进行社会实践,对[25,55]年龄段的人群随机抽取n人进行了一次“你是否喜欢骑车锻炼”的问卷,将被调查人员分为“喜欢骑车”和“不喜欢骑车”,得到如下统计表和各年龄段人数频率分布直方图:
近几年骑车锻炼越来越受到人们的喜爱,男女老少踊跃参加,我校课外活动小组利用春节放假时间进行社会实践,对[25,55]年龄段的人群随机抽取n人进行了一次“你是否喜欢骑车锻炼”的问卷,将被调查人员分为“喜欢骑车”和“不喜欢骑车”,得到如下统计表和各年龄段人数频率分布直方图:| 组数 | 分组 | 喜欢骑车锻炼的人数 | 占本组的频率 |
| 第一组 | [25,30) | 120 | 0.6 |
| 第二组 | [30,35) | 195 | p |
| 第三组 | [35,40) | 100 | 0.5 |
| 第四组 | [40,45) | a | 0.4 |
| 第五组 | [45,50) | 30 | 0.3 |
| 第六组 | [50,55] | 15 | 0.3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com