Question

8．近几年骑车锻炼越来越受到人们的喜爱，男女老少踊跃参加，我校课外活动小组利用春节放假时间进行社会实践，对[25，55]年龄段的人群随机抽取n人进行了一次“你是否喜欢骑车锻炼”的问卷，将被调查人员分为“喜欢骑车”和“不喜欢骑车”，得到如下统计表和各年龄段人数频率分布直方图：

组数	分组	喜欢骑车锻炼的人数	占本组的频率
第一组	[25，30）	120	0.6
第二组	[30，35）	195	p
第三组	[35，40）	100	0.5
第四组	[40，45）	a	0.4
第五组	[45，50）	30	0.3
第六组	[50，55]	15	0.3

（1）补全频率分布直方图，并n，a，p的值；
（2）从[40，50）岁年龄段的“喜欢骑车”中采用分层抽样法抽取6人参加骑车锻炼体验活动，求其中选取2名领队来自同一组的概率．

Answer 1

分析 （1）根据频率分步直方图的面积是这组数据的频率，做出频率，除以组距得到高，画出频率分步直方图的剩余部分，根据频率，频数和样本容量之间的关系，做出n、a、p的值．
（2）采用分层抽样法抽取6人，[40，45）岁中有4人，[45，50）岁中有2人．由此能求出选取2名领队来自同一组的概率．

解答 解：（1）第二组的频率为1-（0.04+0.04+0.03+0.02+0.01）×5=0.3
∴高为$\frac{0.3}{5}=0.06$，频率直方图如下：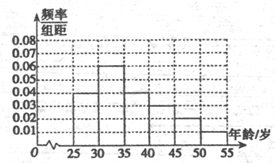

第一组的人数为$\frac{120}{0.6}=200$，频率为0.04×5=0.2，∴$n=\frac{200}{0.2}=1000$．
由题可知，第二组的频率为0.06×5=0.3，
∴第二组的人数为1000×0.3=300，∴$p=\frac{195}{300}=0.65$．
第四组的频率为0.03×5=0.15，∴第四组的人数为1000×0.15=150，∴a=150×0.4=60．
∵[40，45）年龄段的“喜欢骑车”与[45，50）年龄段的“喜欢骑车”的比值为60：30=2：1，
∴采用分层抽样法抽取6人，[40，45）抽有4人，[45，50）中有2人．
由于从6人中选取2人作领队的所有可能情况共${C}_{6}^{2}$=15种，
其中从[40，45）岁中的4人中选取2名领队的情况有6种，
从[45，50）岁中的4人中选取2名领队的情况有1种
所以选取的2名领队来自同一组的概率$P=\frac{7}{15}$．

点评 本题考查频率分步直方图，考查频数，频率和样本容量之间的关系，考查等可能事件的概率，考查利用列举法来得到题目要求的事件数，本题是一个概率与统计的综合题目．