
【题目】已知函数![]() ,
,![]() .
.
(1)若函数![]() 在区间
在区间![]() 上单调递减,试探究函数
上单调递减,试探究函数![]() 在区间
在区间![]() 上的单调性;
上的单调性;
(2)证明:方程![]() 在
在![]() 上有且仅有两解.
上有且仅有两解.
【答案】(1)单调递减.(2)见解析
【解析】
(1)对![]() 求导,
求导,![]() ,再对
,再对![]() 求导,可得
求导,可得![]() 递减区间,可得
递减区间,可得![]() 的取值范围,可得函数
的取值范围,可得函数![]() 在区间
在区间![]() 上的单调性;
上的单调性;
(2)令![]() ,因为
,因为![]() ,可令
,可令![]() ,对其求导,可得
,对其求导,可得![]() 的单调性和零点,记正零点为
的单调性和零点,记正零点为![]() ,可得
,可得![]() 的性质及
的性质及![]() 的表达式,将
的表达式,将![]() 满足的条件代入
满足的条件代入![]() ,综合分析可得证明.
,综合分析可得证明.
解:(1)依题意,![]() ,由
,由![]() ,
,
故函数![]() 的递减区间为
的递减区间为![]() ;而当
;而当![]() 时,
时,![]()
故若函数![]() 在区间
在区间![]() 上单调递减,
上单调递减,
函数![]() 在区间
在区间![]() 上也是单调递减.
上也是单调递减.
(2)令![]() ,
,
因为![]() ,由
,由![]() 得
得![]() ,
,
令![]() ,则
,则![]() ,
,
因为![]() ,且
,且![]() ,所以
,所以![]() 必有两个异号的零点,记正零点为
必有两个异号的零点,记正零点为![]() ,
,
则![]() 时,
时,![]() ,
,![]() 单调递减;
单调递减;![]() 时,
时,![]() ,
,![]() 单调递增,若
单调递增,若![]() 在
在![]() 上恰有两个零点,则
上恰有两个零点,则![]() ,
,
由![]() 得
得![]() ,
,
所以![]() ,又因为
,又因为![]() 的对称轴为
的对称轴为![]() ,
,
所以![]() ,
,
所以![]() ,所以
,所以![]() ,
,
又![]() ,
,
设![]() 中的较大数为
中的较大数为![]() ,则
,则![]() ,
,
故当![]() 时,方程
时,方程![]() 在
在![]() 上有且仅有两解.
上有且仅有两解.


科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为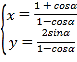 (
(![]() 为参数).以
为参数).以![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,直线
轴的正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() (
(![]() ),将曲线
),将曲线![]() 向左平移2个单位长度得到曲线
向左平移2个单位长度得到曲线![]() .
.
(1)求曲线![]() 的普通方程和极坐标方程;
的普通方程和极坐标方程;
(2)设直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,求
两点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,新能源汽车技术不断推陈出新,新产品不断涌现,在汽车市场上影响力不断增大.动力蓄电池技术作为新能源汽车的核心技术,它的不断成熟也是推动新能源汽车发展的主要动力.假定现在市售的某款新能源汽车上,车载动力蓄电池充放电循环次数达到2000次的概率为85%,充放电循环次数达到2500次的概率为35%.若某用户的自用新能源汽车已经经过了2000次充电,那么他的车能够充电2500次的概率为______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (k为常数,
(k为常数,![]() 且
且![]() ).
).
(1)在下列条件中选择一个________使数列![]() 是等比数列,说明理由;
是等比数列,说明理由;
①数列![]() 是首项为2,公比为2的等比数列;
是首项为2,公比为2的等比数列;
②数列![]() 是首项为4,公差为2的等差数列;
是首项为4,公差为2的等差数列;
③数列![]() 是首项为2,公差为2的等差数列的前n项和构成的数列.
是首项为2,公差为2的等差数列的前n项和构成的数列.
(2)在(1)的条件下,当![]() 时,设
时,设![]() ,求数列
,求数列![]() 的前n项和
的前n项和![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为:
的参数方程为:![]() (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为:
的极坐标方程为:![]() .
.
(Ⅰ)求直线![]() 与曲线
与曲线![]() 公共点的极坐标;
公共点的极坐标;
(Ⅱ)设过点![]() 的直线
的直线![]() 交曲线
交曲线![]() 于
于![]() ,
,![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,离心率为
中,离心率为![]() 的椭圆
的椭圆![]() 的左顶点为
的左顶点为![]() ,过原点
,过原点![]() 的直线(与坐标轴不重合)与椭圆
的直线(与坐标轴不重合)与椭圆![]() 交于
交于![]() 两点,直线
两点,直线![]() 分别与
分别与![]() 轴交于
轴交于![]() ,
, ![]() 两点.若直线
两点.若直线![]() 斜率为
斜率为 ![]() 时,
时, ![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)试问以![]() 为直径的圆是否经过定点(与直线
为直径的圆是否经过定点(与直线![]() 的斜率无关)?请证明你的结论.
的斜率无关)?请证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】大约在20世纪30年代,世界上许多国家都流传着这样一个题目:任取一个正整数![]() ,如果它是偶数,则除以2;如果它是奇数,则将它乘以3加1,这样反复运算,最后结果必然是1.这个题目在东方被称为“角谷猜想”,世界一流的大数学家都被其卷入其中,用尽了各种方法,甚至动用了最先进的电子计算机,验算到对700亿以内的自然数上述结论均为正确的,但却给不出一般性的证明.例如取
,如果它是偶数,则除以2;如果它是奇数,则将它乘以3加1,这样反复运算,最后结果必然是1.这个题目在东方被称为“角谷猜想”,世界一流的大数学家都被其卷入其中,用尽了各种方法,甚至动用了最先进的电子计算机,验算到对700亿以内的自然数上述结论均为正确的,但却给不出一般性的证明.例如取![]() ,则要想算出结果1,共需要经过的运算步数是( )
,则要想算出结果1,共需要经过的运算步数是( )
A.9B.10C.11D.12
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com