
已知函数
(1)若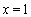 为
为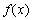 的极值点,求
的极值点,求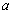 的值;
的值;
(2)若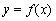 的图象在点
的图象在点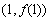 处的切线方程为
处的切线方程为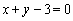 ,
,
①求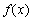 在区间
在区间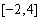 上的最大值;
上的最大值;
②求函数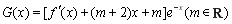 的单调区间.
的单调区间.
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业七十二第十章第九节练习卷(解析版) 题型:解答题
一个口袋装有n个红球(n≥5且n∈N)和5个白球,一次摸奖从中摸2个球(每次摸奖后放回),2个球颜色不同则为中奖.
(1)试用n表示一次摸奖中奖的概率.
(2)若n=5,求3次摸奖的中奖次数ξ=1的概率及数学期望.
(3)记3次摸奖恰有1次中奖的概率为P,当n取多少时,P最大?
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业七十七选修4-4第一节练习卷(解析版) 题型:解答题
已知曲线C:ρsin(θ+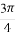 )=
)=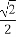 ,曲线P:ρ2-4ρcosθ+3=0,
,曲线P:ρ2-4ρcosθ+3=0,
(1)求曲线C,P的直角坐标方程.
(2)设曲线C和曲线P的交点为A,B,求|AB|.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业七十一第十章第八节练习卷(解析版) 题型:选择题
设随机变量ξ的概率分布为P(ξ=i)=a( )i,i=1,2,3,则a的值是( )
)i,i=1,2,3,则a的值是( )
(A)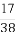 (B)
(B)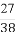 (C)
(C)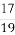 (D)
(D)
查看答案和解析>>
科目:高中数学 来源:2014年高中数学全国各省市理科导数精选22道大题练习卷(解析版) 题型:解答题
已知向量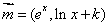 ,
,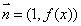 ,
,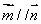 (
(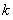 为常数,
为常数, 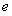 是自然对数的底数),曲线
是自然对数的底数),曲线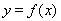 在点
在点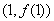 处的切线与
处的切线与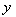 轴垂直,
轴垂直,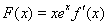 .
.
(Ⅰ)求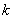 的值及
的值及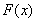 的单调区间;
的单调区间;
(Ⅱ)已知函数 (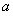 为正实数),若对于任意
为正实数),若对于任意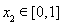 ,总存在
,总存在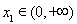 , 使得
, 使得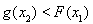 ,求实数
,求实数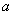 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2014年陕西省咸阳市高考模拟考试(一)理科数学试卷(解析版) 题型:解答题
如图,四边形PCBM是直角梯形,∠PCB=90°,PM∥BC,PM=1,BC=2.又AC=1,∠ACB=120°,AB⊥PC,直线AM与直线PC所成的角为60°.
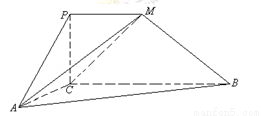
(1)求证:PC⊥AC;
(2)求二面角M﹣AC﹣B的余弦值;
(3)求点B到平面MAC的距离.
查看答案和解析>>
科目:高中数学 来源:2014年陕西省咸阳市高考模拟考试(一)理科数学试卷(解析版) 题型:选择题
抛物线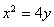 的焦点坐标是( )
的焦点坐标是( )
A.(2,0) B.(0,2) C.(l,0) D.(0,1)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com