
一个口袋装有n个红球(n≥5且n∈N)和5个白球,一次摸奖从中摸2个球(每次摸奖后放回),2个球颜色不同则为中奖.
(1)试用n表示一次摸奖中奖的概率.
(2)若n=5,求3次摸奖的中奖次数ξ=1的概率及数学期望.
(3)记3次摸奖恰有1次中奖的概率为P,当n取多少时,P最大?
(1) P=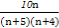 (2)
(2) 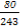
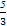 (3) n=20
(3) n=20
【解析】(1)记“1次从n+5个球中摸出2个球”为事件A,card(A)=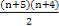 .
.
“1次从n+5个球中摸出2个球且2个球异色”为事件B,card(B)=5n,
所以,所求概率P=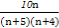 .
.
(2)3次放回式摸奖中“每次从n+5个球中摸出2个球且2个球异色”为独立重复事件,
当n=5时,获奖次数ξ~B(3,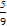 ),
),
P(ξ=1)=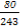 .
.
E(ξ)=np=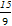 =
=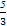 .
.
(3)ξ~B(n,p),
P(ξ=1)=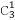 p(1-p)2=3p3-6p2+3p,0<p<1,
p(1-p)2=3p3-6p2+3p,0<p<1,
令f(p)=3p3-6p2+3p,由f'(p)=9p2-12p+3=0,
得p=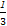 ;
;
当p=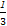 时f(p)有最大值.
时f(p)有最大值.
由p=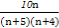 =
=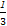 ,解得n=20.
,解得n=20.
所以当n=20时,3次摸奖恰有1次中奖的概率最大.


科目:高中数学 来源:2014年高考数学全程总复习课时提升作业三十一第五章第二节练习卷(解析版) 题型:解答题
等差数列{an}的各项均为正数,其前n项和为Sn,满足2S2=a2(a2+1),且a1=1.
(1)求数列{an}的通项公式.
(2)设bn=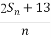 ,求数列{bn}的最小值项.
,求数列{bn}的最小值项.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业七十六选修4-2第三节练习卷(解析版) 题型:解答题
已知2×2矩阵M=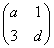 有特征值λ=-1及对应的一个特征向量e1=
有特征值λ=-1及对应的一个特征向量e1=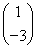 .
.
(1)求矩阵M.
(2)设曲线C在矩阵M的作用下得到的方程为x2+2y2=1,求曲线C的方程.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业七十八选修4-4第二节练习卷(解析版) 题型:解答题
设直线l1的参数方程为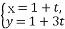 (t为参数),直线l2的方程为y=3x+4,求l1与l2间的距离.
(t为参数),直线l2的方程为y=3x+4,求l1与l2间的距离.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业七十二第十章第九节练习卷(解析版) 题型:填空题
设一次试验成功的概率为p,进行100次独立重复试验,当p=_______时,成功次数的标准差的值最大,其最大值为 .
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业七十二第十章第九节练习卷(解析版) 题型:选择题
若随机变量X~B(100,p),X的数学期望E(X)=24,则p的值是( )
(A) (B)
(B) (C)
(C)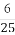 (D)
(D)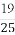
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业七十三第十章第十节练习卷(解析版) 题型:填空题
调查了某地若干户家庭的年收入x(单位:万元)和年饮食支出y(单元:万元),调查显示年收入x与年饮食支出y具有线性相关关系,并由调查数据得到y对x的回归直线方程: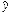 =0.254x+0.321.由回归直线方程可知,家庭年收入每年增加1万元,年饮食支出平均增加 万元.
=0.254x+0.321.由回归直线方程可知,家庭年收入每年增加1万元,年饮食支出平均增加 万元.
查看答案和解析>>
科目:高中数学 来源:2014年高中数学全国各省市理科导数精选22道大题练习卷(解析版) 题型:解答题
已知函数
(1)若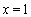 为
为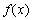 的极值点,求
的极值点,求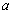 的值;
的值;
(2)若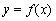 的图象在点
的图象在点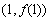 处的切线方程为
处的切线方程为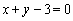 ,
,
①求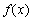 在区间
在区间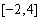 上的最大值;
上的最大值;
②求函数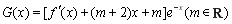 的单调区间.
的单调区间.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com