
定义两个实数间的一种新运算“*”:x*y=ln(ex+ey),x,y∈R.当x*x=y时,x=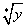 .对任意实数a,b,c,给出如下命题:
.对任意实数a,b,c,给出如下命题:
①a*b=b*a;
②(a*b)+c=(a+c)*(b+c);
③(a*b)-c=(a-c)*(b-c);
④(a*b)*c=a*(b*c);
⑤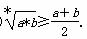
其中正确的命题有________.(写出所有正确的命题序号)
①②③④⑤
解析 因为a*b=ln(ea+eb),b*a=ln(eb+ea),
所以a*b=b*a,即①对;
因为(a*b)+c=ln(ea+eb)+c=ln[(ea+eb)ec]
=ln(ea+c+eb+c)=(a+c)*(b+c),所以②对;
只需令②中的c为-c,即有结论(a*b)-c=(a-c)*(b-c),所以③对;
因为(a*b)*c=[ln(ea+eb)]*c=ln[ +ec]
+ec]
=ln(ea+eb+ec),
a*(b*c)=a*[ln(eb+ec)]=ln[ea+ ]
]
=ln(ea+eb+ec),
所以(a*b)*c=a*(b*c),即④对;
设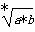 =x,则x*x=a*b,
=x,则x*x=a*b,
所以ln(ex+ex)=ln(ea+eb),
所以2×ex=ea+eb,
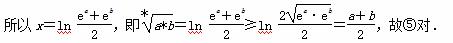 故正确的命题是①②③④⑤.
故正确的命题是①②③④⑤.


科目:高中数学 来源: 题型:
条件甲:“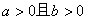 ”,条件乙:“方程
”,条件乙:“方程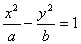 表示双曲线”,那么甲是乙的( )
表示双曲线”,那么甲是乙的( )
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com