
分析 (Ⅰ)通过an+1=an2-nan+1、a1=3代入计算即得结论;
(Ⅱ)先证明n=1时不等式成立,再假设n=k时不等式成立,进而论证n=k+1时,不等式依然成立,最终得到不等式an≥n+2恒成立.
解答 解:(Ⅰ)依题意,a2=a12-a1+1=32-3+1=7,
a3=a22-2a2+1=72-2×7+1=36,
a4=a32-3a3+1=362-3×36+1=1189;
(Ⅱ)结论:an≥n+2的关系.
用数学归纳法证明如下:
①当n=1时,a1=3=1+2,不等式成立;
②假设当n=k(k≥2)时不等式成立,即ak≥k+2,
那么ak+1=ak(ak-k)+1
≥(k+2)(k+2-k)+1
=2k+5
≥k+3,
也就是说,当n=k+1时,ak+1≥(k+1)+2;
由①、②可知:对于所有n≥1,有an≥n+2.
点评 本题考查数列的通项,考查数列归纳法,注意解题方法的积累,属于中档题.


 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:高中数学 来源: 题型:选择题
| A. | 矩形 | B. | 菱形 | C. | 平行四边形 | D. | 任意四边形 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
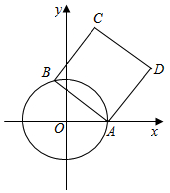 已知圆O为单位圆:x2+y2=1,点A(1,0),B为单位圆上的动点,如图,以AB为边作正方形ABCD,求动点D的轨迹方程及OD的取值范围.
已知圆O为单位圆:x2+y2=1,点A(1,0),B为单位圆上的动点,如图,以AB为边作正方形ABCD,求动点D的轨迹方程及OD的取值范围.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com