
| A. | 矩形 | B. | 菱形 | C. | 平行四边形 | D. | 任意四边形 |
分析 把给出的向量等式变形,可得($\overrightarrow{AB}-\overrightarrow{CD}$)•$\overrightarrow{BC}$=0,($\overrightarrow{AB}-\overrightarrow{CD}$)•$\overrightarrow{DA}$=0,有$\overrightarrow{BC}$∥$\overrightarrow{AD}$,从而得到AD∥BC.同理可得AB∥CD.再由($\overrightarrow{AB}-\overrightarrow{CD}$)•$\overrightarrow{BC}$=0,$\overrightarrow{AB}$∥$\overrightarrow{CD}$,
得AB⊥BC,则四边形ABCD为矩形.
解答 解:由$\overrightarrow{AB}$$•\overrightarrow{BC}$=$\overrightarrow{BC}$$•\overrightarrow{CD}$=$\overrightarrow{CD}$$•\overrightarrow{DA}$=$\overrightarrow{DA}$$•\overrightarrow{AB}$,
得($\overrightarrow{AB}-\overrightarrow{CD}$)•$\overrightarrow{BC}$=0,($\overrightarrow{AB}-\overrightarrow{CD}$)•$\overrightarrow{DA}$=0,
∴$\overrightarrow{BC}$∥$\overrightarrow{AD}$,即AD∥BC.
同理有AB∥CD,则四边形ABCD为平行四边形,
又($\overrightarrow{AB}-\overrightarrow{CD}$)•$\overrightarrow{BC}$=0,$\overrightarrow{AB}$∥$\overrightarrow{CD}$,
∴AB⊥BC,则四边形ABCD为矩形.
故选:A.
点评 本题考查平面向量的数量积运算,考查了平面向量的加减法,是中档题.


科目:高中数学 来源: 题型:选择题
| A. | 48 | B. | 72 | C. | 84 | D. | 168 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 钝角三角形 | B. | 锐角三角形 | C. | 等腰三角形 | D. | 直角三角形 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
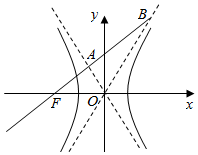 如图,已知双曲线$\frac{x^2}{a^2}$-$\frac{y^2}{b^2}$=1(a>0,b>0)的左焦点为F,过F作斜率为1的直线交双曲线的渐近线于A,B两点,且|OB|=2|OA|,则该双曲线的离心率为$\sqrt{10}$.
如图,已知双曲线$\frac{x^2}{a^2}$-$\frac{y^2}{b^2}$=1(a>0,b>0)的左焦点为F,过F作斜率为1的直线交双曲线的渐近线于A,B两点,且|OB|=2|OA|,则该双曲线的离心率为$\sqrt{10}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com